Những Thời Khắc Trọng Đại của TOÁN HỌC- Bài 10

10 . Nhà thi sĩ- toán học của Khorasan

Howard Eves

Trần Quang Nghĩa lược dịch

Trong nửa sau của thế kỉ 11, ba người trẻ tuổi Ba Tư, thông minh và có năng lực, cùng tùng học với một trong những người hiền triết nhất thành Khorasan là Imam Mowaffak. Ba thanh niên đó là – Nizam, Hasan và Omar Khayyam – trở thành ba bạn thân thiết. Thời đó người ta tin rằng các học trò của Ngài Imam thế nào cũng thành đạt nên Hasan một hôm đề nghị với hai bạn, họ sẽ cùng nhau kết nghĩa và thề thốt rằng, trong ba người, nếu có người nào gặp được vận lớn thì sẽ chia đều may mắn cho hai người kia. Năm tháng trôi qua, Nizam trở thành người gặp hồng phúc, khi ông trở thành tể tướng dưới triều vua Alp Arslan. Không bỏ lỡ cơ hội, hai người bạn bèn tìm đến và nhắc lại lời thề xưa thuở còn đi học.

Hasan xin một chức quan và được nhà vua đồng ý qua sự giới thiệu của Tể tướng Nizam. Nhưng là một người ích kỹ và vô ơn, Hasan mưu tính hất cẳng Nizam nhưng bất thành, bị giáng chức và trục xuất. Còn Omar, vốn không màng đến tước vị hoặc chức vụ, chỉ xin phép được sống trong bóng mát vận hội của ngài tể tướng, nơi ông có thể quảng bá khoa học và toán học và cầu nguyện cho bạn mình lộc thọ dồi dào. Cảm kích trước tấm chân thành và sự khiêm cung của bạn, ngài tể tướng chu cấp cho Omar mọi tài vật giúp ông thỏa chí nguyện.

Sau nhiều phen bôn ba và lận đận, cuối cùng Hasan trở thành thủ lĩnh một nhóm cuồng tín, chiếm đóng thành Alamut năm 1090 trong vùng núi non phía tây biển Caspian. Dùng thành làm pháo đài và nơi xuất phát những trận đột kích các đoàn thương buôn qua lại. Hasan và đồng bọn gieo rắc kinh hoàng khắp thế giới Hồi giáo. Hasan được gán bí danh “lão già vùng núi”, và một trong vô số nạn nhân của y là người bạn thân thời trẻ Nizam.

Trái ngược với cuộc đời bão tố và hủy diệt của Hasan, cuộc đời của Omar yên tĩnh và xây dựng. Ông sống yên bình và đóng góp một cách xứng đáng cho nền văn thơ và khoa học của thời đại ông.

Bài viết này nhằm tuyên dương một thành tựu toán học nổi bật của học giả Omar – một thành tựu đáng được gọi là MỘT THỜI KHẮC TRỌNG ĐẠI CỦA TOÁN HỌC. Trước tiên xin nhắc lại vài khái niệm nền tảng.

Gọi là phương trình đa thức thực một ẩn x là phương trình có dạng:

a_oxⁿ + a₁xⁿ ^– ¹ + . . . + a_n _– ₁x + a_n = 0

trong đó n là số nguyên dương và a₀, a₁, . . ., a_n là những số thực với a_o khác 0. Một giá trị của x thỏa mãn phương trình được gọi là nghiệm của phương trình. Một trong những nhiệm vụ chính yếu của đại số thời cổ là tìm ra phương pháp tổng quát tìm nghiệm của phương trình, gọi là giải phương trình ấy. Vì thời xưa ta chỉ biết đến số thực dương, do đó trong khoảng mấy trăm năm qua, giải phương trình chỉ là tìm nghiệm thực dương của nó, nếu có. Số n được gọi là bậc của phương trình.

Việc giải phương trình bậc 1 bằng phương pháp đại số hay hình học đều không mấy khó khăn. Nếu phương trình bậc 1 một ẩn có nghiệm dương thì nó luôn có thể đưa về dạng: ax = b, trong đó a, b là những số dương. Về đại số, nghiệm là x = b/a. Về hình học, x là số tỉ lệ thứ tư đối với ba độ dài a, b và 1, nghĩa là a : b = 1 : x , và x có thể được xác định bằng thước và compa trong phép dựng cho bởi hình dưới (trên), trong đó COD là một góc bất kì, OA = a, OB = b, AC = 1, và CD được kẻ song song với AB.

Điều thú vị là người Ai cập cổ giải phương trình bậc 1 bằng một phương pháp mà sau này người Âu châu gọi là qui tắc giả sử. Theo đó, để giải phương trình: x + x /7 = 24, ta giả sử x = 7, thế thì x + x/7 = 8, thay vì 24. Vì 8 nhân 3 là 24, do đó x phải bằng 3 x7 = 21.

Mặc dù phương trình bậc 2 phức tạp hơn phương trình bậc 1 nhưng các nhà toán học thời cổ cũng giải được phương trình này bằng phương pháp đại số và hình học. Cách giải đại số bằng phương pháp phân tích bình phương hay giải bằng công thức mọi học sinh trung học đều đã nắm. Người Babylon cổ cách đây 4000 năm đều đã biết cả hai phương pháp giải này.

Người Hy lạp giải bằng hình học phương trình bậc 2: x² – px + q = 0 như sau (hình trên, dưới):

Dựng nửa đường tròn đường kính AB = p.
Dựng đường thẳng song song và cách đường kính một khoảng là q. Đường này cắt đường tròn tại M.
Kẻ MH vuông góc AB thế thì nghiệm của phương trình là độ dài đoạn AH hay BH.

Phương trình bậc 3 là một bài toán thử thách. Người Babylon dùng bảng tính các giá trị của n³ + n² với một số giá trị của n để giải một số phương trình bậc 3 đặc biệt.

Archimedes, trong một tài liệu còn lưu truyền, đã khảo sát điều kiện để một phương trình bậc 3 có nghiệm dương. Còn phương pháp giải phương trình bậc 3 tổng quát chỉ được biết đến vào thế kỉ thứ 16 do một nhà toán học Ý tìm ra. Phép giải phương trình bậc 3 bằng phương pháp hình học được tìm ra sớm hơn 5 thế kỉ, vào thế kỉ thứ 11, bởi nhà thi sĩ-toán học Ba tư là Omar Khayyam đã kể trên.

Thời kì từ khi Đế quốc La mã sụp đổ vào giữa thế kỉ thứ 5 đến thế kỉ thứ 11 được gọi là thời đại Đen Tối của Âu châu, bởi vì trong thời gian này nền văn minh và học thuật của Âu châu xuống đến mức thấp nhất. Tuy nhiên lúc này lại là thời kì vàng son của đế quốc Ả rập. Trong vòng một thập kỷ sau khi nhà tiên tri Mohammed chạy từ Mecca đến Medina vào năm 623, các bộ tộc Bedouin chia rẻ và phân tán khắp các bán đảo Ả rập đã tập hợp lại vững chắc bằng niềm tin tôn giáo nhiệt thành để trở thành một quốc gia hùng mạnh. Trong vòng một thế kỷ, các lực lượng vũ trang dưới bóng ngọn cờ vàng xanh của đạo Hồi đã mở rộng vùng thống trị của ngôi sao và trăng lưỡi liềm vươn đến tận Ấn độ, qua Ba tư, Mesopotamia, và Bắc Phi sang tận Tây Ban Nha.

Điều quan trọng bậc nhất cho việc gìn giữ kho tàng văn minh nhân loại là thái độ năng nổ của người Ả rập khi họ thâu tóm sự uyên bác của nền văn minh Hy lạp và Ấn độ. Nhiều công trình Ấn Hi về y học, thiên văn, và toán học đã được chuyên cần dịch sang tiếng Ả rập và nhờ thế còn được lưu truyền, và sau này các học giả Âu châu dịch lại sang tiếng Latin và các ngôn ngữ khác. Nếu không nhờ công lao to lớn của các học giả Ả rập thì phần lớn các công trình khoa học Ấn Hy đã vĩnh viễn biệt tăm trong thời kỳ tăm tối Trung Cổ. Ngoài công lao vĩ đại giữ gìn tri thức nhân loại, người Ả rập còn có sự đóng góp của riêng mình, và độc đáo nhất là công trình của Omar Khayyan liên quan đến việc giải phương trình bậc 3 bằng phương pháp hình học.

Omar Khayyan (1044-1123) là một thi sĩ, nhà thiên văn, và toán học Ba tư, sinh ra và học tập tại thành phố Naishapur thuộc Khorasan (đông bắc Iran ngày nay). Ông đã từng được yêu mến và ca tụng trong thế giới phương Tây qua những vầng thơ mỹ lệ trong quyển The Rubaiyat do Edward Fitzgerald chuyển ngữ. Trong thế giới khoa học, ông cũng được biết đến qua công trình cải tạo bộ lịch thêm chính xác, sự luận bàn của ông về tiên đề song song của Euclid cho thấy ý tưởng ông đi trước cả ý tưởng của Saccheri, ý tưởng mà sau này dẫn đến việc hình thành môn hình học phi Euclid, và đặc biệt là đóng góp của ông trong nền đại số Ả rập là việc tìm nghiệm dương của mọi phương trình bậc 3 bằng phương pháp hình học.

Hãy minh họa các bước giải của Omar Khayyan cho phương trình dưới đây: x³ + b² x + a³ = cx²

trong đó a, b, c, x là các độ dài. Omar phát biểu bài toán này như sau: “một lập phương, một cạnh nào đó và một số nào đó bằng một bình phương nào đó.” Nói một cách hình học, bài toán này được phát biểu như sau: Cho các độ dài a, b, c, hãy dựng một đoạn thẳng x sao cho đẳng thức trên thỏa mãn. Mục tiêu là dựng độ dài x bằng thước và compa càng nhiều càng tốt. Chứ chỉ dùng thước và compa mà thôi thì thường không giải được. Tại một vài bước dựng, ta được phép vẽ các đường cônic hoàn toàn xác định nào đó.

Phép dựng cơ bản được dùng nhiều lần trong bài toán này là dựng đoạn tỉ lệ thứ tư với ba đoạn đã biết. Đây là bài toán cổ mà người Hy lạp xưa đã biết. Giả sử u, v, w là ba độ dài đã biết, hãy dựng độ dài x sao cho : u : v = w : x . Hình bên, tương tự như hình trang trước, là cách dựng độ dài x bằng thước và compa độ dài x cần tìm.

Bây giờ ta bắt tay giải hình học phương trình bậc 3 của Omar Khayyan nói trên:

x³ + b² x + a³ = cx²

Đầu tiên ta tìm đoạn z sao cho b : a = a : z bằng phép dựng đoạn tỉ lệ thứ tư đã nói. Tiếp theo, lần nữa, dựng đoạn m sao cho: b : z = a : m.

Như vậy : m = a³/b².

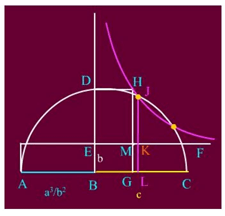
Bây giờ, xem hình dưới, dựng AB = m = a³/b² và BC = c. Dựng nửa đường tròn đường kính AC. Đường vuông góc với AC tại B, cắt nửa đường tròn tại D.

Trên BD, lấy đoạn BE = b và qua E kẻ EF song song AC.

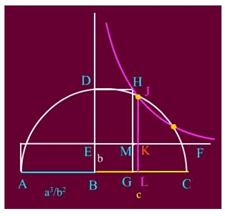
Bằng cách dựng đoạn tỉ lệ thứ tư, ta dựng G trên BC sao cho ED : BE = AB : BG và vẽ hình chữ nhật DBGH.

Qua H vẽ hyperbol vuông góc có EF và ED là hai tiệm cận (tức đối với hệ trục mà EF và ED là trục hoành và trục tung thì phương trình của hyperbol là xy = hằng số).

Hyperbol này cắt nửa đường tròn tại J, và qua J vẽ đường song song với DE, cắt EF tại K và BC tại L.

Gọi M là giao điểm của GH và EF. Thế thì:

Vì J và H trên hyperbol nên : EK. KJ = EM. MH
Vì ED : BE = AB : BG, ta có: BG. ED = BE. AB
Do đó, từ 1 và 2: EK. KJ = EM. MH = BG. ED = BE. AB
Lại có :
LJ = EK. (BE + KJ)

= EK. BE + EK. KJ

= EK. BE + AB . BE (theo 3)

= BE. (EK + AB)

= BE. AL

=> BL². LJ² = BE². AL².

Mà LJ² = AL. LC ( hệ thức lượng trong tam giác vuông)
Do đó, từ 4 và 5:

BE². AL = BL². LC

<=> BE².(BL + AB) = BL². (BC – BL)

Đặt BE = b, AB = a³/b² và BC = c vào đẳng thức 6, ta được :

b²(BL + a³/b²) = BL² (c – BL)

Khai triển và thu gọn, ta được:

BL³ + b². BL + a³ = c. BL²

và do đó BL = x là một nghiệm của phương trình đã cho. Vì hyperbol cắt nửa đường tròn tại hai điểm L nên phương trình này có 2 nghiệm dương.

Phải công nhận là phương pháp của Omar thật tinh tế và khéo léo. Nhận xét rằng ta có thể vẽ hyperbol bằng phương pháp vẽ từng điểm một và điểm này cũng vẽ bằng phương pháp đoạn tỉ lệ thứ tư. Thật vậy nếu gọi N là một điểm bất kì trên hyperbol qua H nói trên, gọi P là hình chiếu của N lên EF thì:

MH = EN. NP

<=> EN : EM = MH : NP,

và NP chính là đoạn tỉ lệ thứ tư của ba đoạn đã biết là EN, EM và MH. Bằng cách này ta có thể vẽ nhiều điểm của hyperbol và nối lại thì được đường hyperbol liền lạc. Omar còn giải nhiều dạng phương trình bậc 3 khác bằng phương pháp tương tự.

Omar Khayyan mất tại Naishapur năm 1123. Một đệ tử của ông, Khwajah Nizami, kể rằng thời sinh tiền, trong những lần đàm đạo với thầy Omar ngoài vườn, thường nghe thầy tâm sự muốn phần mộ của mình sau này tọa lạc tại nơi nào mà gió đông về sẽ rắc những cánh hồng lả tả rơi lên mộ. Vài năm sau ngày thầy mất, người học trò cũ có dịp qua Naishapur, liền tìm đến thăm thầy. Y trông thấy ngôi mộ thầy nằm bên cạnh một khu vườn. Từ bờ tường, những cành hoa khoe sắc không ngừng rắc những cánh hoa lả tả lên phần mộ một vĩ nhân trong khi tấm mộ bia thì hoàn toàn bị che khuất.