Những Thời Khắc Trọng Đại của TOÁN HỌC- Bài 7

7 . Nhà tư tưởng và viên tướng

Howard Eves

Trần Quang Nghĩa lược dịch

Thật đáng kinh ngạc khi có nhiều thành tựu toán học có nguồn gốc từ Hy Lạp cách đây hai ngàn năm. “Nơi miền đất đó có những người khổng lồ”, theo như cách nói của nhà hình học Julian Lowell Coolidge của Harvard. Không còn nghi ngờ gì nữa nhân vật vĩ đại nhất trong số các người khổng lồ là Archimedes của thành phố Syracuse, nhà toán học kiệt xuất. Trong bài này ta sẽ thấy, bằng những phương tiện rất hạn chế, Archimedes đã tìm ra diện tích của những tam giác cong và thể tích vài mặt tròn xoay, mở đường cho phép tính vi tích phân mà mãi nhiều năm sau mới tiến hoá và hoàn thiện qua các công trình của Kepler, Cavalieri, Fermat, Wallis, Barrow, Leibniz, và Newton.

Archimedes, một cư dân của thành phố Syracuse, Hy lạp trên đảo Sicily, sinh vào khoảng năm 287 TCN và chết trong trận tấn công của quân La Mã năm 212 TCN vào thành phố. Ông là con một nhà thiên văn được vua Hieron của Syracuse sủng ái. Ông có thể đã sống vài năm tại Đại Học Alexandria ở Ai Cập vì ông thường nhắc đến tên ba người bạn là Conon, Dositheus và Eratosthenes, đều là thành viên của Đại Học. Nhiều công trình toán học của ông đã được trao đổi qua thư từ với ba người kế nghiệp đầy năng lực này của Euclid.

Nhiều câu chuyện đầy màu sắc vể Archimedes đã được các sử gia La Mã thuật lại. Chẳng hạn chuyện ông chế tạo những cỗ máy giúp phòng thủ thành Syracuse trong hai năm bi vây hãm bởi quân La Mã dưới sự chỉ huy của tướng Marcellus. Đó là những máy bắn đá có thể điều chỉnh tầm bắn, và di chuyển được trên bệ phóng có bánh xe đến vị trí tuỳ ý trên tường thành và bắn những tảng đá nặng nề về phía những chiến thuyền địch đang đến gần. Đó là những cần cẩu với hệ thống ròng rọc phức tạp có thể móc vào thuyền địch và nhấc bổng chúng lên khỏi mặt nước, đập vỡ chúng ra từng mảnh. Đó là những mảnh gương thủy tinh khổng lồ dùng ánh sáng mặt trời hội tụ để đốt cháy những cánh buồm của quân xâm lược. Và câu phát biểu đầy tính khoa trương của ông: “Hãy cho tôi một điểm tựa, tôi sẽ nhấc bổng quả đất” có thể tin được khi người ta đã từng chứng kiến cảnh ông ngồi thoải mái trên bãi biển, một tay quay cần nhẹ nhàng và hệ thống ròng rọc phức hợp chuyển động từ từ kéo chiến thuyền từ ụ trên cảng xuống biển.

Như những nhà toán học lớn khác, Archimedes có sức tập trung trí tuệ rất cao, và không chú ý gì đến ngoại cảnh vây quanh. Câu chuyện nổi tiếng nhất là việc ông suy nghĩ để tìm ra lời giải bài toán đố của nhà vua Hieron nhờ ông tìm xem người thợ kim hoàn có gian lận (pha đồng vào vàng ) khi làm chiếc vương miện bằng vàng, với điều kiện là ông không được làm méo mó gì đến vật quí này. Và lời giải đã chớp loè trong trí khi ông đang tắm trong nhà tắm công cộng, ông vui mừng đến nổi đứng bật dậy, lao ra đường, quên cả mặc quần áo, và la toáng lên: “Eureka, eureka.” (Tôi đã tìm ra, đã tìm ra). Cái mà ông tìm ra là định luật về sức đẩy mang tên ông.

Archimedes đã tìm ra nhiều định lí hình học bằng những hình vẽ trên lớp tro của lò sưởi hoặc trên lớp dầu mỏng dùng để bôi sau khi tắm. Thực tế, theo các sử gia La Mã ông đã ra đi khi đang mải mê làm toán với hình vẽ trên sa bàn, trong khi quân xâm lược đã chọc thủng hàng phòng vệ của thành Syracuse. Khi thấy bóng một tên lính La Mã xông vào, che mất hình vẽ của mình, ông đã la lớn, bảo hắn tránh ra và nhận một ngọn giáo kết liễu đời mình.

Mười công trình của Archimedes được truyền lại cho hậu thế chúng ta, và một vài trước tác đã thất lạc. Những tuyệt tác được lưu truyền toàn là những luận thuyết toán học, được viết một cách súc tích, hoàn hảo, độc đáo, thể hiện kỹ năng tính toán và chứng minh nghiêm nhặt. Có lẽ đóng góp quan trọng nhất của toán học trong những công trình này là ý tưởng khơi mào cho phép tính vi tích phân đến gần 2000 năm sau. Chúng ta sẽ bàn kỹ về thành tựu này.

Một vài trang bản thảo của Archimedes cho thấy phương pháp ông vận dụng tương tự như quá trình tính tích phân thực sự. Lấy hai trong những bản thảo này làm minh học. Thứ nhất là bản thảo: Về hình cầu và hình trụ, và thứ hai là bản thảo mơí phát hiện gần đây có tên là Phưong Pháp Luận. Bản thảo đầu chứa tổng cộng 60 định lí, trong đó xuất hiện lần đầu tiên công thức tính diện tích mặt cầu, đới cầu một đáy và thể tích khối cầu và khối đới cầu một đáy. Kết quả về diện tích và thể tích hình cầu là hệ quả của định lí 33 và 34: Hình trụ có đáy bằng với đường tròn lớn của mặt cầu và chiều cao bằng đường kính mặt cầu thì có diện tích toàn phần bằng 3/2 diện tích mặt cầu và có thể tích bằng 3/2 thể tích khối cầu. Từ kết quả này ta suy ra được công thức quen thuộc: S = 4πr² và V = 4πr³/3 của diện tích S và V của hình cần bán kính r.

Đó là một chuỗi lí luận gồm những bước sắp xếp khéo léo dẫn đến những kết quả nhuộm màu tích phân, trong đó thay vì phương pháp trực tiếp hiện đại tinh tế sử dụng lấy giới hạn, ta bắt gặp một phương pháp gián tiếp và hơi nặng nề, nhưng cũng hiệu quả, gọi là phương pháp vét cạn Eudoxious, qua đó Archimedes đã tìm được công thức diện tích và thể tích hình cầu. Nhưng ta không trình bày phép chứng minh này, mà thay vào đó chúng ta trình bày chi tiết bản thảo đã được Archimedes ghi lại trong cuốn Phương Pháp Luận, trong đó ông kể làm thế nào ông đã tìm ra công thức đó.

Cuốn Phương Pháp Luận là một bản thảo bị thất lạc rất lâu, chỉ được biết đến do người đời sau nhắc lại, cho đến khi nhà toán sử người Đức nổi tiếng Heiberg tìm ra một bản sao chép của quyển gốc vào năm 1906. Bản sao chép viết trên giấy palimpsest – đó là một lọai giấy mà sau khi tẩy rữa mực in người ta có thể dùng lại. Tuy nhiên sau một thời gian dài lớp chữ đầu tiên của bản thảo Phương Pháp Luận lại tái xuất hiện dưới lớp chữ mới. Bản viết này là bức thư của Archimedes gởi cho cho Eratosthenes ở Đại Học Alexandria, báo tin ông tìm ra công thức diện tích và thể tích hình cầu là bằng phương pháp cân bằng.

Muốn thế ông cắt hình cầu ra thành vô số lát nhỏ bằng những mặt phẳng song song, rồi treo nó tại một đầu của đòn bẩy sao cho nó cân bằng với một khối mà trọng tâm đã được biết rõ. Hãy minh họa ý tưởng này trong bài toán tính thể tích của Archimedes.

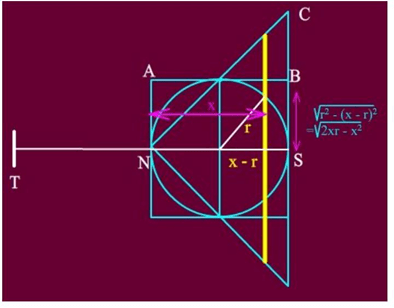
Gọi r là bán kính hình cầu. Đặt hình cầu với đường kính nằm ngang theo trục hòanh, với cực bắc N nằm ở gốc. Dựng hình trụ và hình nón bằng cách quay hình chữ nhật NABS kích thước 2r x r và tam giác NCS vuông cân quanh trục hòanh. Bây giờ cắt ra từ ba khối những lát mỏng thẳng đứng cách N một khỏang x và có độ dày là Δx. Thể tích của các miếng này xấp xỉ bằng:

từ khối cầu : πx(2r – x)Δx

từ khối trụ : πr²Δx

từ khối nón : πx²Δx
Mang những miếng cắt ra từ hình cầu và hình nón rồi treo nó với tâm ở điểm T, trong đó TN = 2r. Momen của hai khối này đối với N là:

[πx(2r – x)Δx + πx²Δx]2r

= 4πr²x Δx

tức bằng 4 lần momen của miếng cắt ra từ hình trụ khi miếng đó ở nguyên vị trí. Cộng một số lớn các miếng này với nhau, ta được:

2r[thể tích khối cầu + thể tích khối nón] = 4r[thể tích khối trụ]
hay

2r[thể tích khối cầu + 8πr³/3]

= 8πr⁴
Suy ra:

thể tích khối cầu = 4πr³/3

Đây là cách mà Archimedes khám phá công thức thể tích khối cầu. Nhưng lương tri toán học không cho phép ông nhận phương pháp này là cách chứng minh đúng đắn, và vì thế sau đó ông đã dùng phương pháp vét cạn để chứng minh.

Trong phương pháp cân bằng này ta nhìn thấy một ý tưởng phì nhiêu khi xem một đại lượng là tổng vô hạn của những thành phần vi tế. Với ngôn ngữ hiện đại của giới hạn, phương pháp này chính là ý tưởng nền tảng của phép tính tích phân. Với quan điểm này, công trình của Archimedes xứng đáng được gọi là MỘT THỜI KHẮC TRỌNG ĐẠI CỦA TOÁN HỌC.

Archimedes quá thích thú với công trình Về hình cầu và hình trụ đến nổi ông bày tỏ ước nguyện sau khi chết bia mộ ông được khắc phù điêu hình cầu nội tiếp trong hình trụ. Tướng Marcellus, để tỏ lòng trân trọng một bậc anh tài, sau khi chinh phục Syracuse, đã chôn cất ông trọng thể và cho xây dựng mộ bia đúng như sở nguyện của ông. Nhiều năm sau, khi Cicero, giữ chức thuế quan cho chính quyền La Mã, đến Syracuse công tác, không ai còn nhớ đến địa điểm của ngôi mộ. Sau nhiều ngày truy tìm, ông đã tìm được mộ bia nằm lăn lóc trong đám cỏ rậm. Ông cho dựng lại và sửa sang mộ phần. Nhưng rồi trải qua năm tháng, ngôi mộ cũng bị lãng quên, và với đà phát triển của thành phố, nó đã biệt vô âm tín.

Tuy nhiên, vào năm 1965, trong khi đào móng cho công trình xây dựng một khách sạn mới ở Syracuse, cần cẩu mang lên một tấm bia cổ trên đó có khắc một hình trụ ngọai tiếp một hình cầu. Và một lần nữa, mộ bia của nhân vật Syracuse kiệt xuất nhất đã được tìm thấy.