Nghiên Cứu Lịch Sử

6 . Kinh Thánh của Toán Học

 Howard Eves

Trần Quang Nghĩa lược dịch

 Sau khi Đại Đế Alexander băng hà năm 323 TCN, toàn bộ đế quốc Macedonia được phân thành ba phần, và phần đất chứa Ai cập đặt dưới quyền cai trị của vị tướng tài năng của Alexander là Ptolemy Soter, không lâu sau đã lên ngôi vua của miền đất này. Ptolemy chọn Alexandria, chỉ cách cửa sông Nile một vài dặm, làm thủ đô, và vào khoảng năm 300 TCN, ông mở cửa trường Đại Học Alexandria lừng danh. Trong số những học giả uyên bác có mặt trong ban giảng huấn là nhà toán học Euclid, chắc chắn cũng đã từng theo học tại Học Viện Platonic ở Athens.

Một trong những nhiệm vụ quan trọng về Toán học của Euclid khi dạy tại Alexandria là biên soạn bộ Elements (Các Yếu Tố) lừng danh thiên cổ của ông. Bộ sách đáng nể và đồ sộ này gồm 13 quyển, là bộ sách toán được viết theo phương pháp tiên đề đầu tiên truyền tụng đến chúng ta. Nó được xem là một   dấu ấn lớn lao trong lịch sử phát triển toán học, mà tầm ảnh hưởng của nó đến các công trình khác về sau không thể nói hết được .

Các Yếu Tố của Euclid chắc chắn là MỘT THỜI KHẮC TRỌNG ĐẠI CỦA TOÁN HỌC. Bộ sách tổng hợp quá đầy đủ các công trình trước đây đến nổi không ai còn nhớ đến những thành quả có trước và chúng ta chỉ biết đến chúng qua các lời chú giải của các tác giả về sau này. Từ khi bộ sách ra đời, Các Yếu Tố đã nhận được bao nhiêu là lời tán tụng. Trừ Thánh Kinh, không có trước tác nào đã được sử dụng, học tập, hoặc biên tập lại rộng rãi đến như vậy trong hơn hai ngàn năm thống trị mọi giáo trình giảng dạy hình học. Hơn 1000 lần xuất bản từ khi nó xuất hiện lần đầu năm 1482. Nội dung và phương pháp của nó đã tạo một cú hích lớn lao cho sự phát triển nội dung cũng như nên tảng luận lý của toán học. Proclus, một nhà toán học sống vào thế kỷ thứ năm, đã làm sáng tỏ cho chúng ta ý nghĩa của từ Yếu Tố. Các Yếu Tố trong nghiên cứu chứng minh là các định lí nền tảng được dùng nhiều trong môn học; giúp chứng minh hầu hết các định lí khác. Chức năng của chúng có thể so sánh với bảng chữ cái đối với ngôn ngữ; thật ra chữ cái trong tiếng Hy Lạp cũng được gọi là Các Yếu Tố. Việc chọn ra định lí nào là yếu tố của môn học đòi hỏi một sự phán xét khéo léo tính tế của tác giả.

Không phải vì đã có những nỗ lực trước Euclid mà ta xem thường công trình rực rỡ của ông. Theo Proclus, Các Yếu Tố đã được biên soạn đầu tiên bởi Hippocrates ở thành Cios vào giữa thế kỷ thứ 5 TCN. Sau đó đến Leon, giữa thời Plato và Eudoxus, đóng góp thêm nhiều định lí hữu dụng so với Hippocrates. Bộ sách giáo khoa dùng tại Học Viện Platonic được tổng hợp bởi Theudias, được coi như là một tuyển tập đáng nể của Các Yếu Tố. Công trình của Theudias hiển nhiên là tiên phong so với trước tác của Euclid, chắc chắn ông đã tham khảo bộ sách này vì người ta cho rằng ông đã từng học tại Học Viện Platonic một thời gian. Euclid cũng quen thuộc với công trình của Theudias và Eudoxus, nhưng không vì thế mà tác phẩm của ông bớt đi giá trị. Mặc dù tác phẩm này là tập hợp những biên soạn của những người đi trước, nhưng giá trị chủ yếu của bộ sách nằm ở sự việc tuyển chọn khéo léo và sắp xếp hợp lí và sắc sảo các kiến thức theo một chuỗi lôgic của sự phát triển từ một nhóm nhỏ các tiên đề ban đầu. Cũng không vì dưới ánh sáng phê phán của các bộ óc toán học hiện đại cho thấy bộ sách đã bộc lộ những khiếm điểm ở cấu trúc hệ thống, mà giá trị của bộ sách bị giảm sút đi. Không thể nào, vào một thời xa xưa và phôi thai của khoa học, có thể tạo ra một hệ thống toán học hoàn hảo, không tì vết.

Hiện nay nguyên bản của bộ Elements ở thời ông không còn tồn tại. Tất cả những ấn phẩm hiện đại của Các Yếu Tố đều dựa vào bộ hiệu đính của Theon ở Alexandria, một nhà phê bình Hy Lạp sống khoảng 700 năm sau thời đại của Euclid. Chỉ khi bắt đầu thế kỷ thứ 19 người ta mới phát hiện một bản sao cổ hơn. Năm 1808, khi Napoleon ra lệnh chuyển tất cả những bản thảo quí từ các thư viện Ý về Pháp, F. Peyrard tìm thấy, trong thư viện toà thánh Vatican, một bản sao từ thế kỷ thứ 10 của tác phẩm Các Yếu Tố của Euclid.

Nghiên cứu bản này cho thấy chỉ có sự khác biệt nho nhỏ so với bộ sách hiệu đính của Theon. Bản dịch ra Latin Các Yếu Tố không phải từ tiếng Hy Lạp mà từ tiếng Ả Rập. Vào thế kỉ thứ tám một số bản thảo vùng Byzantine Hy Lạp được Ả rập chuyển ngữ; và vào năm 1120, Adelard, một học giả Anh đã dịch ra Latinh từ bản thảo này. Những bản dịch khác từ Ả rập ra Latin là do Gherardo (1114-1187), và 150 năm sau Adelard, là bản dịch của Johannes Campanus. Ấn phẩm  đầu tiên của bộ sách là vào năm 1482 in tại Venise dựa trên bản dịch của Campanus. Bộ sách quí hiếm này được đóng thật đẹp và là quyển sách toán đầu tiên được in ra. Bản dịch ra Latinh từ tiếng Hy Lạp do Commandino thực hiện năm 1572. Bản này là căn bản cho các bản dịch về sau, bao gồm tác phẩm quan trọng của Simson, từ đó nhiều tác phẩm khác đã tham khảo.

Nhà toán học Pháp, Legendre (1752-1833), nổi tiếng trong lịch sử chủ yếu nhờ công trình về lý thuyết số, hàm elliptic, phương pháp bình phương cực tiểu, và tích phân, cũng quan tâm đến vấn đề sư phạm. Trong tác phẩm rất phổ thông Các Yếu Tố Hình Học, ông đã cải tiến tính sư phạm của bộ Các Yếu Tố của Euclid bằng cách sắp xếp lại và đơn giản nhiều định lí của Euclid. Công trình này rất được ưa chuộng tại Mỹ và trở thành nguồn tham khảo cho các sách giáo khoa hình học tại đó. Bản dịch ra tiếng Anh của cuốn Các Yếu Tố Hình Học được thực hiện năm 1819 bời John Farrar của Đại Học Harvard. Ba năm sau, một bản dịch khác được nhà văn Thomas Carlyle thực hiện. Ông đã từng là thầy giáo dạy toán trước khi trở thành nhà văn.

Trong bản hiệu đính của Theo, bộ Elements gồm 13 quyển, và chứa tất cả 465 định lí. Trái với ấn tượng ban đầu, ngoài hình học, còn đề cập đến lý thuyết số cơ bản và đại số Hy lạp.

Quyền I bắt đầu với những định nghĩa và giải thích cần thiết, tiên đề, định đề. Mặc dù các nhà toán học ngày nay coi thuật ngữ tiên đề và đinh đề là một, một số nhà toán học Hy lạp, trong đó có Euclid, thì phân biệt hai thuật ngữ này, như sau: tiên đề là một giả định đầu tiên hiển nhiên đối với mọi ngành nghiên cứu, trong khi định đề là một giả định đầu tiên liên hệ đến ngành đặc biệt nào đó đang xét. Những định lí của Quyển I là những định lí quen thuộc về điều kiện bằng nhau của tam giác, đường thẳng song song và các đa giác. Định lí 47 và 48, hai định lí cuối cùng của quyển, là định lí Pythagoras thuận và đảo. Điều này làm ta nhớ lại một câu chuyện của triết gia Anh, Thomas Hobbes (1588-1679). Một ngày, mở Các Yếu Tố của Euclid, tình cờ đọc phải định lí Pythagoras, Hobbes thốt lên: “Trời đất, điều này không thể được,” và rồi tiếp tục đọc các cách chứng minh trong Quyển I, đi ngược trở lên đến các tiên đề và định đề, ông mới bắt đầu bị thuyết phục.

Quyền II, một quyển mỏng chỉ có 14 định lí, liên hệ đến các hệ thức lượng của trường phái Pythagoras. Chúng ta đã bàn đến, trong bài 4, về định lí 12 và 13 của quyển này là sự tổng quát hóa Pythagoras thành định lí hàm số cosin.

Quyển III, gồm 39 định lí, chứa những định lí quen thuộc về đường tròn, dây cung, cát tuyến, tiếp tuyến và số đo các góc nội tiếp, góc trong và ngoài mà bất cứ học sinh trung học nào cũng học qua. Quyển IV, với chỉ 16 định lí, đề cập đến các phép dựng, bằng thước và compa, các loại đa giác đều nội tiếp trong đường tròn cho trước.

Quyển V, như đã bàn đến ở bài trước, đề cập đến lý thuyết của Eudoxus vể tỉ lệ. Quyển này được coi là một trong những kiệt tác của văn chương toán học. Trong bài trước, chúng ta đã từng kể đến chuyện, nhờ đọc quyển này mà nhà toán học Bolzano đã thoát khỏi cơn bệnh tật khi du lịch ở Prague. Quyển VI, một trong những quyển phong phú nhất của bộ Các Yếu Tố, áp dụng 1ý thuyết Eudoxus vào việc nghiên cứu các hình đồng dạng.

Quyển VII, VIII và IX, chứa tổng cộng 102 định lí, đề cập đến lý thuyết số cơ bản. Quyển VII bắt đầu với thuật toán mà ngày nay chúng ta đặt tên là thuật toán Euclidean, tìm ước số chung lớn nhất của hai hay nhiều số nguyên. Chúng ta cũng tìm gặp các lý thuyết trước đây của Pythagoras về tì lệ. Quyển VIII bàn về tỉ số, tỉ lệ và cấp số nhân. Quyển IX chứa nhiều định lí có ý nghĩa về lý thuyết số. Định lí 14 trong quyển này tương đương với định lí nền tảng số học như sau : Mọi số nguyên lớn hơn 1 có thể phân tích thành tích các thừa số nguyên tố và cách phân tích này là duy nhất. Trong định lí 20, ta bắt gặp cách chứng minh đẹp đẽ rằng số các số nguyên tố là vô hạn. Định lí 35 cung cấp một cách giải hình học của tổng các số hạng của một cấp số nhân, và định lí cuối cùng của quyển này, định lí 36, thiết lập một công thức cho ta những số hoàn hảo (Perfect number: là một số nguyên dương mà tổng các ước nguyên dương thực sự của nó bằng chính nó. Chẳng hạn số 6 là số hoàn hảo nhỏ nhất vì các ước số thực sự của nó là 1, 2, và 3 mà 1 + 2 + 3 = 6).

Quyển X là quyển sách khó đọc nhất, bàn về số vô tỉ đó là những độ dài vô ước với những độ dài cho trước. Ba quyển cuối cùng đề cập đến hình học không gian, gồm những kiến thức ta quen thuộc ở thời trung học, không có các công thức về hình cầu. Trong bài sau, chúng ta sẽ biết rằng các kiến thưc về hình cầu là do Archimedes phát hiện thêm về sau này.

Cũng còn có những bản thảo Hy Lạp thời cổ khác, ngoài bộ Elements, được truyền lại cho hậu thế chúng ta. Chẳng hạn những công trình sâu sắc của Archimedes, tác phẩm Thiết Diện Cônic của Apollonius, Almagest của Ptolemy, Metrica của Heron, Số Học của Diophantus, Tuyển Tập Toán Học của Pappus, và còn nhiều nữa. . . Nếu chỉ muốn tìm trong số những tác phẩm ấy một ứng viên duy nhất để vinh danh thì Các Yếu Tố của Euclid là tác phẩm duy nhất xứng đáng là MỘT THỜI KHẮC TRỌNG ĐẠI CỦA TOÁN HỌC.

Chúng ta sẽ khép lại bài này bằng cách liệt kê vài tiên đề và định đề Euclid:

Tiên đề hoặc những Khái Niệm Chung

1. Những vật cùng bằng với một vật khác thì bằng nhau.
2. Nếu những vật bằng nhau cộng thêm vào hai vật bằng nhau thì bằng nhau.
3. Nếu những vật bằng nhau lấy ra từ hai vật bằng nhau thì bằng nhau.
4. Những vật mà chồng khít nhau thì bằng nhau.
5. Toàn thể thì lớn hơn thành phần.

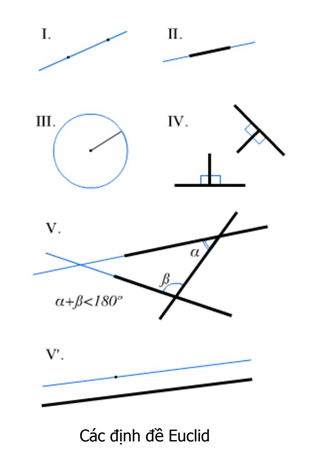
Định đề

1. Qua hai điểm cho trước có thể dựng được một đường thẳng.
2. Một đường thẳng có thể kéo dài liên tục về cả hai phía.
3. Có thể dựng được một đường tròn có tâm là điểm cho trước và qua một điểm khác cho trước
4. Mọi góc vuông đều bằng nhau.
5. Nếu một đường thẳng xác định với hai đường thẳng khác hai góc trong cùng bên có tổng nhỏ hơn hai góc vuông thì chúng sẽ cắt nhau tại một điểm nằm về phía hai góc ấy.

Cần nhận xét rằng cách dựng trình bày trong ba định đề đầu được giới hạn chỉ dùng compa và thước không chia đơn vị . Đó là lí do tại sao hai công cụ này thường được gọi là công cụ Euclidean, và phép dựng với hai công cụ trên mà thôi được gọi là phép dựng Euclidean. Euclid thường dùng phép dựng để chứng minh sự tồn tại của một thực thể nào đó vừa được định nghĩa. Ví dụ khi định nghĩa đường phân giác của một góc là đường qua đỉnh góc và chia góc ấy thành hai góc bằng nhau, không có gì bảo đảm là đường phân giác ấy tồn tại. Để chứng minh nó tồn tại, đơn giản nhất là chỉ ra cách dựng nó. Các định lí về sự tồn tại trong toán học rất quan trọng, và cách dựng một thực thể là cách thỏa mãn nhất để chứng minh thực thể ấy tồn tại.

Trong thực tế tồn tại những thực thể mà phép dựng chúng vượt quá công cụ Euclidean, và những nổ lực để tìm ra những cách dựng mà giờ đây ta biết là không thể dựng được chỉ bằng thước và compa đã cho ra đời một lượng kiến thức đáng kể của hình học.

Chúng ta cũng biết rằng định đề thứ 5 của Euclid, sau này vào thế kỉ thứ 19, đã tạo cảm hứng đưa đến một sáng tạo có tầm quan trọng cực kì về mặt phát triển toán học. Cassius J. Keyser đã cho rằng định đề này là một phát biểu tuy ngắn gọn và giản dị nhưng lại là phát biểu nổi tiếng nhất trong lịch sử khoa học.