Nghiên Cứu Lịch Sử

4. Định lí lớn đầu tiên

 Howard Eves

Trần Quang Nghĩa lược dịch

 Một trong những định lí hấp dẫn, và chắc chắn là quan trọng và hữu dụng nhất của hình học sơ cấp chính là định lí Pitago, nói rằng : “Trong một tam giác vuông bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”. Nếu có định lí nào xứng đáng được phong tặng MỘT THỜI KHẮC TRỌNG ĐẠI CỦA TOÁN HỌC thì định lí Pitago chính là ứng viên số một, vì định lí này chắc chắn là định lí lớn đầu tiên trong toán học. Nhưng khi chúng ta đi truy tìm nguồn gốc của định lí, chúng ta vấp phải một quá trình không mấy gì chắc chắn. Mặc dù giai thoại cho rằng định lí này là của Pythagoras, một nghiên cứu kỹ lưỡng các chữ hình nêm trong bản đất sét khai quật được ở Mesopotamia đã phát giác rằng chính những người Babylone cổ khoảng một ngàn năm trước thời đại Pythagoras đã biết đến định lí này. Định lí này cũng đã được người Ấn và Trung Hoa thời cổ biêt đến, muộn nhất cũng là cùng thời với Pythagoras. Tuy nhiên không có chứng minh định lí nào được đưa ra, do đó có thể Pythagoras hay một thành viên nào đó trong hội kín lừng danh này là người đầu tiên đã chứng minh được định lí.

Chúng ta hãy dừng lại một chút để nói về Pythagoras và hội kín này của ông. Pythagoras là người thứ hai được chỉ đích danh trong lịch sử Toán học. Nhìn kỹ qua màn sương bí ẩn của quá khứ, chúng ta biết rằng Pythagoras sinh vào khoảng 572 TCN trên đảo Aegean, Samos, không xa Miletus, quê hương của Thales. Nhỏ hơn Thales năm mươi tuổi và sống không xa ông, có thể Pythagoras đã học toán với ông. Cũng như Thales, ông chắc đã đến Ai Cập cư trú một thời gian, và sau đó có thể du lịch đến nhiều nơi khác, có thể đến tận Ấn độ. Trở về nhà sau hai năm lang bạt, ông chứng kiến Samos bị thống trị dưới ách độc tài của Polycrates và phần lớn Ionia nằm dưới ách đô hộ của người Ba tư, và vì thế ông di cư đến hải cảng Crotona của   Hy Lạp ở tận phía nam nước Ý. Tại đây ông thành lập trường Pythagorean nổi tiếng, bề ngoài là học viện nghiên cứu triết lí, toán học và khoa học tự nhiên, bên trong là một hội kín huynh đệ với những nghi lễ và nội quy thần bí. Dần dần quyền lực chính trị và các khuynh hướng quý tộc của hội đã trở nên lớn mạnh đến nổi các thế lực dân chủ của miền nam nước Ý đã đập phá trường học và các huynh đệ phải ly tán khắp nơi. Theo sử liệu, Pythagoras chạy đến Metapontum và mất tại đó, có thể bị kẻ thù sát hại, lúc đó ông khoảng 75 hay 80 tuổi. Các huynh đệ, mặc dù tứ tán, vẫn tiếp tục tồn tại ít nhất hai thế kỷ nữa.

Triết lí của Pythagoras, thoang thoảng nguồn gốc Ấn, dựa trên giả định rằng những số nguyên là tác nhân tạo ra những chất lượng khác nhau của con người và vật chất; nói tóm lại, số nguyên thống trị thế giới về chất cũng như về lượng. Khái niệm thăng hoa vai trò của số nguyên đã dẩn đến việc nghiên cứu nó một cách sâu xa; bởi vì biết đâu, nhờ việc vén màn bí mật tìm ra những tính chất thâm thúy của số nguyên, con người có thể, đến một mức nào đó, hướng đạo hoặc chuyển đổi vận mệnh của mình.

Và vì hình học có liên hệ với con số, nên hình học cũng được nghiên cứu một cách nghiêm túc. Do lối dạy của Pythagoras chủ yếu là truyền miệng, và theo luật kín của hội mọi khám phá toán học đều phải vinh danh người sáng lập Pythagoras, do đó không thể biết được ai chính là tác giả đích thực của định lí này.

Trở lại THỜI KHẮC TRỌNG ĐẠI đang bàn đến, ta tự hỏi không biết nó đã được chứng minh như thế nào. Có rất nhiều ức đoán về vấn đề này và phần lớn đều cho rằng cách chứng minh có thể dựa vào cách cắt xén như sau:

Gọi a, b, c lần lượt là hai cạnh và cạnh huyền của tam giác vuông và xét hai hình vuông có cạnh là a + b như hình trên. Hình vuông thứ nhất được chia thành sáu miếng gồm hai hình vuông và bốn tam giác vuông đều bằng với tam giác ban đầu. Hình vuông thứ hai được chia thành năm miếng gồm bốn tam giác vuông cùng bằng với tam giác ban đầu và một hình vuông cạnh bằng cạnh huyền c. Bằng cách loại bỏ khỏi hai hình vuông bốn tam giác vuông bằng nhau, ta suy ra diện tích hình vuông có cạnh bằng cạnh huyền thì bằng tổng diện tích hai hình vuông có cạnh là cạnh góc vuông, tức

c² = a² + b².

Để chứng minh miếng chính giữa của hình thứ hai là hình vuông cạnh c, ta phải dựa vào tính chất tổng ba góc của tam giác vuông thì bằng hai góc vuông. Nhưng tính chất này đối với bất cứ tam giác nào cũng đã được cho là của Pythagoras. Vì phép chứng minh tính chất này đòi hỏi phải biết các tính chất về tính song song, những thành viên của hội Pythagoras cũng được vinh danh về kết quả hình học này.

Có lẽ không có định lí hình học nào nhận được nhiều cách chứng minh hơn định lí Pythagoras.

Trong quyển sách của ông, tác giả E. S. Loomis đã thu thập và phân loại hơn 370 cách chứng minh định lí nổi tiếng này.

Phép chứng minh thường dùng cách phân tích hai hình thành tổng hay hiệu các hình có diện tích bằng nhau từng đôi một. Cách mà ta đã dùng trên đây là phân tích theo hiệu.

Hình dưới là một lối chứng minh theo tổng do Perigal tìm ra năm 1873 mà không biết là Qorra đã biết hơn một ngàn năm trước.

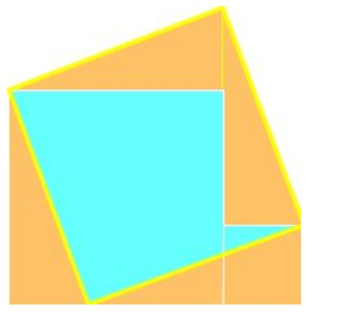
Còn cách sắp xếp như hình dưới để chứng minh định lí là của Leonardo da Vinci (1425-1519). Hai đa giác giới hạn bởi các cạnh xanh và các cạnh trắng thì có diện tích bằng nhau vì bằng 2 lần diện tích các tứ giác bằng nhau. Nếu loại khỏi hai hình này hai tam giác bằng nhau có kích thước a, b, c thì ta được các hình còn lại cũng tương đương, tức: a² + b² = c².

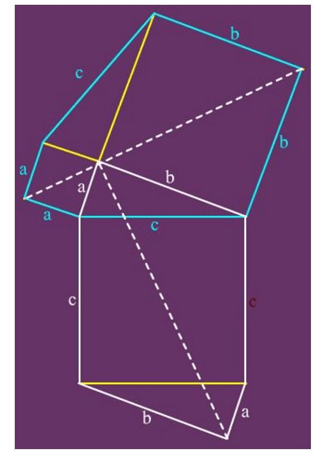
Cách chứng minh đẹp đẽ của định lí này được Euclid trình bày trong Định lí 47 Quyển I của bộ Elements dựa vào hình vẽ bên dưới. Tóm tắt như sau:

AC²  = 2S_JAB  = 2S_CAD  = S_ADKL

Chứng minh tương tự:

BC² = S_BEKL

Do đó : AC² + BC² = S_ADKL + S_BEKL  

                                = AB² (đpcm)

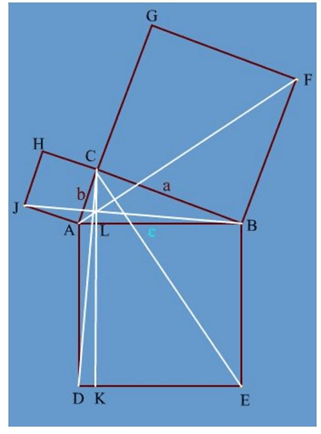
Nhà toán học Ả rập Bhaskara đã chứng minh định lí Pythagoras theo cách chúng ta đã học ở hình học sơ cấp.

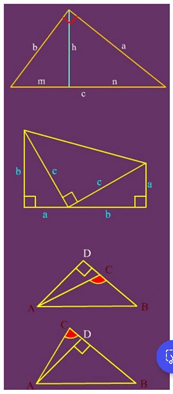
Sử dụng tỉ số đồng dạng của các cặp tam giác như hình trên (trên), ta có:

    c/b = b/ m và c/ a = a/ n

Suy ra : am = b² va cn = a²

Cộng lại ta được:

      a² + b² = c(m + n) = c²

Cách chứng minh này đã được nhà toán học John Wallis (1616-1703) phát hiện lại.

James Abram Garfield (1831-1881), tổng thống thứ hai mươi của Mỹ, khi còn là nghị sĩ, đã tìm được một cách chứng minh định lí này như trong hình trên (giữa). Cho diện tích hình thang bằng tổng diện tích các tam giác vuông, ta được :

(a + b). (a + b)/2 = ab/2 + ab/2 +      

                                   c²/2

<=> a² + 2ab + b² = 2ab + c²

<=> a² + b² = c²

Như   nhiều   định lí lớn khác, định lí Pythagoras có phần mở rộng của nó, chẳng hạn:

(1) Trong một tam giác vuông, diện tích một hình dựng lên cạnh huyền bằng tổng diện tích hai hình đồng dạng với nó dựng lần lượt trên hai cạnh góc vuông.

(2) Trong một tam giác bình phương một cạnh đối diện với góc tù (nhọn) bằng tổng bình phương hai cạnh kia cộng ( trừ) với hai lần tích của một cạnh với hình chiếu của cạnh kia lên cạnh đó (2 hình trên bên dưới cùng)

AB² = BC² + CA² + 2.BC. DC (C tù) AB² = BC² + CA² – 2.BC. DC (C nhọn)

Đây thật ra là định lí hàm số cosin trong tam giác ABC, trong cả hai trường hợp ta đều có:

AB² = BC² + CA² – 2.BC.CAcosC

(3) Có lẽ sự mở rộng đáng chú ý nhất là của Pappus thành Alexandria (300) trong thời cổ Hy Lạp ở trang đầu của Quyển IV bộ Tuyển Tập Toán của ông, như sau:

Gọi ABC là tam giác bất kì và CADE, CBFG là các hình bình hành dựng trên cạnh CA, CB và bên ngoài tam giác. DE và FG cắt nhau tại H, kẻ AL và BM song song và bằng HC. Thế thì diện tích hình bình hành ABML bằng tổng diện tích các hình bình hành CADE và CBFG (Hình dưới trên).

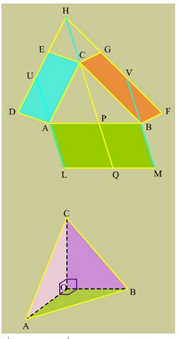
Chứng minh không có gì là khó khăn:

S_CADE = S_CAUH = S_PQLA

 S_CBFG = S_CBVH = S_QMBP

Cộng lại, ta được đpcm.

(4) Một hướng mở rộng của định lí Pythagoras là từ mặt phẳng đến không gian. Hình tam giác vuông trong mặt phẳng xem ra tương ứng một hình chóp tam giác OABC mà ba mặt tại O đều vuông (hình trên dưới). Trong hình chóp như thế ta có:

(S_OAB)² + (S_OBC)² + (S_OCA)² = (S_ABC)²

(thường được gọi dưới tên định lí Gua)

Trong không khí càng ngày ngày càng nhộn nhịp các cuộc thám hiểm không gian, các nhà khoa học càng tỏ ra bức xúc đến việc nhắn tin đến các sinh vật ngoài trái đất sự hiện diện của loài người chúng ta. Người ta nghĩ ngay đến một kiến trúc khổng lồ tiêu biểu khiến các trí khôn ngoài trái đất có thể hiểu được dễ dàng có sự hiện diện của một trí khôn khác trên hành tinh Trái Đất. Kiến trúc được ưu ái nhất chính là mô hình của định lí Pythagoras xây dựng trên sa mạc Sahara hay đồng cỏ nước Nga.

Năm 1971, nước Nicaragua phát hành một loạt tem vinh danh “mười định lí toán học quan trọng nhất” của nhân loại. Mỗi tem mô tả một định lí với một hình vẽ đi kèm và in trên mặt sau một giải thích ngắn gọn bằng tiếng Tây Ban Nha tầm quan trọng của định lí. Một trong những con tem ấy biểu thị định lí Pythagoras “a² + b² = c²“. Các nhà khoa học và toán học hẳn đã rất đổi hãnh diện khi thấy những công thức này nhận được một vinh dư lớn lao như thế. Điều này không có gì phải ngạc nhiên vì chắc chắn những công thức ấy đã đóng góp cho sự phát triển của nhân loại nhiều hơn công trạng của các vị tướng hay các vị vua đã từng được chọn in trên tem.