Những Thời Khắc Trọng Đại của TOÁN HỌC- Bài 3

3. Từ thực nghiệm đến nghiên cứu

Howard Eves

Trần Quang Nghĩa lược dịch

Khoảng năm 600 trước công nguyên toán học bước vào thời kì phát triển thứ ba. Các sử gia về toán học đều nhất trí vinh danh sự tiến bộ vượt bậc này cho người Hi Lạp trong thời đó, và người tiên phong nổi tiếng nhất là Thales thành Miletus, một trong thất hiền thời cổ đại. Hình như Thales trải những năm trẻ tuổi làm nghề buôn bán, sau đó trở nên giàu có, và nhờ thế trong những năm cuối đời, ông mới có thể dành hết thời gian cho nghiên cứu và du lịch. Ông đã từng đến Ai cập và mang về cho thành Miletus những thành tựu của người Ai cập về hình học. Ông là một thiên tài trong nhiều lãnh vực: chính khách, cố vấn, kỹ sư, doanh nhân, triết gia, nhà toán học và thiên văn học. Ông là người đầu tiên mà tên tuổi được biết đến trong lịch sử toán học, và là cá nhân đầu tiên đã nêu ra những phát hiện hình học bằng phương pháp diễn dịch. Những kết quả sau đây là những đóng góp của ông:

Đường kính chia đôi đường tròn.
Hai góc đáy của một tam giác cân thì bằng nhau.
Những góc đối đỉnh tạo bởi hai đường thẳng cắt nhau thì bằng nhau.
Hai tam giác có hai góc bằng nhau và một cạnh bằng nhau thì bằng nhau.
Góc nội tiếp trong nửa đường tròn là một góc vuông.

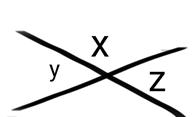
Thật ra chắc chắn năm kết quả trên đã được biết rất lâu trước thời Thales, và năm kết quả này đều có thể kiểm chứng bằng thực nghiệm. Vì thế giá trị của phát hiện này không phải ở nội dung của chúng mà ở chỗ Thales đã chứng thực chúng bằng lí luận chứng minh thay vì bằng trực giác và thực nghiệm. Chẳng hạn, kết quả thứ ba có thể dễ dàng kiểm chứng bằng cách dùng kéo cắt ra cặp góc đối đỉnh và đặt chúng trùng lên nhau. Tuy nhiên Thales đã chứng minh theo cách chúng ta đã học ở trung học. Trong hình dưới, ta muốn chứng minh góc y = góc z. Ta có góc y và góc z cùng bù với góc x, tức x + y = 180° và x + z = 180°. Tức y và z đều băng 180° – x. Mà hai đại lượng cùng bằng một đại lượng thứ ba thì bằng nhau, do đó góc y = góc z.

Kết quả trên được suy ra từ một chuổi diễn dịch nhỏ, dựa vào một kết quả cơ bản hơn. Loại hình học này gọi là hình học chứng minh hay hình học diễn dịch, và đã được người Hi Lạp phát triển mạnh mẽ từ 600 TCN về sau. Những người Hi Lạp này đã dỡ bỏ những thành quả hình học, và nói chung toán học, được xây dựng bằng phương pháp thực nghiệm để thay thế bằng phương pháp nghiên cứu. Nổ lực đầy ý thức và tập trung này chắc chắn là MỘT THỜI KHẮC TRỌNG ĐẠI CỦA TOÁN HỌC, và nếu truyền thống này là đúng, thì Thales ở thành phố Miletus là người phát động đầu tiên.

Câu hỏi là, trong số các dân tộc vào thời đó, tại sao lại là người Hi Lạp, chứ không ai khác, đã khẳng định rằng các chân lí hình học phải được chứng minh bằng lí luận chứ không phải bằng các phép đo thực nghiệm. Câu trả lời có thể là do cái gọi là sự bí ẩn Hy Lạp. Các học giả đã cố gắng cung cấp những giải thích về bí ẩn Hy Lạp, và không có lời giài thích riêng lẻ nào thỏa mãn mà phải xét tất cả các lời giải thích mới đủ làm họ hài lòng. Lời giải thích thông thường nhất là nằm ở khuynh hướng thiên về hoài nghi triết học của người Hy Lạp cổ đại. Trong triết học, người ta quan tâm đến những kết quả không tránh được suy ra từ những giả định, và phương pháp thực nghiệm chỉ là một phép đo có khả năng xác minh kết quả đã biết. Chỉ có phép lí luận diễn dịch mới có thể là công cụ mà các triết gia yêu thích, và vì thế thật là tự nhiên khi người Hi Lạp chuộng phương pháp này hơn khi nghiên cứu hình học.

Một lối giải thích khác về bí ẩn Hy Lạp nằm trong lòng yêu thích cái đẹp của người Hi Lạp, như đã thể hiện hùng hồn trong nền nghệ thuật, thi ca, điêu khắc, và kiến trúc của họ. Sự trân trọng cái đẹp là một kinh nghiệm tri thức cũng như tình cảm, và từ quan điểm này, tính thứ tự, nhất quán, đầy đủ và xác định được tìm thấy trong lối lí luận diễn dịch đã làm họ hài lòng.

Mội lối giải thích khác là nằm trong vai trò của giai cấp nô lệ trong xã hội Hy Lạp thời cổ đại. Giai cấp có đặc quyền sống trên sự phục vụ của tầng lớp nô lệ, từ việc điều hành công cuộc kinh doanh, sản xuất của chủ nhân cho đến việc chăm sóc nhà cửa bằng lao động giản đơn và chân tay. Khuynh hướng bóc lột này đã vô tình tách rời lý thuyết với thực hành, khiến những người đặc quyền vô tình khinh bỉ các hoạt động thực tế và thực nghiệm tay chân, và quay ra ưa thích sự diễn dịch và trừu tượng.

Cuối cùng lời giải thích có thể đến từ những đổi thay mạnh mẽ về chính trị và kinh tế xảy ra trong thời kì đó. Thời đại Đồ Sắt đã đến, chữ viết đã được phát minh, tiền đồng đã được đúc, và những phát hiện về địa lí đã được thực hiện. Thế giới đang sẵn sàng cho một nền văn minh mới, và nền văn minh này đang hình thành trong nhóm người có tư tưởng cấp tiến và sáng tạo trong các thành phố buôn bán mọc lên tấp nập dọc bờ biển Tiểu Á và sau đó trên nội địa Hy lạp, ở Sicily và bờ biển nước Ý. Những thành phố buôn bán này phần lớn là những khu xây dựng của thương nhân Hy Lạp. Trong không khí phát triển của chủ nghĩa duy lí, con người bắt đầu hỏi tại sao cũng như thế nào. Giờ đây những tiến trình thực nghiệm đã hoàn toàn đủ cho câu hỏi thế nào, những chưa đủ để trả lời được tại sao, và những nổ lực sử dụng phương pháp diễn dịch chỉ là để xác quyết nhu cầu khẩn cấp đó.

Nhưng dù bất cứ lối giải thích nào về bí ẩn Hy lạp, ta cũng phải công nhận là họ đã lái hình học đi theo một hướng hoàn toàn khác trước gồm những quy tắc thực nghiệm của tiền nhân. Hơn nữa, sự kiện là những ý tưởng diễn dịch đầu tiên xuất phát từ lĩnh vực hình học chứ không phải từ đại số đã khai trương một truyền thống trong toán học còn duy trì mãi đến tận thời gian gần đây.

Nhưng không vì thế ta có thể nghĩ rằng người Hi lạp tránh xa mọi phương pháp thí nghiệm hay thực nghiệm sơ khởi, bởi vì ít khi nào, nếu muốn nói là không bao giờ, có một phát hiện toán học có ý nghĩa nào mà không bắt đầu bằng những thí nghiệm sơ khởi theo cách này hay cách khác. Trước khi một phát biểu toán học nào có thể được chứng minh hoặc phản chứng minh bằng diễn dịch, đầu tiên nó phải được ức đoán, và một ức đoán không có gì khác hơn là một một dự đoán sinh ra từ trực giác, quan sát, tương tự hoá, thực nghiệm hóa hoặc một dạng thức nào đó có tính kinh nghiệm. Sự diễn dịch là một dạng thức trình bày có tính hình thức và đầy tính thuyết phục, nhưng khó lòng là một phương tiện giúp khám phá, phát minh. Khám phá là một tập hợp những cơ chế phức tạp cần dữ kiện để làm việc và dữ kiện thì thường được cung cấp qua những quan sát thực nghiệm.

Ngay cả những bước lí luận diễn dịch cũng không tự đến qua chính cơ chế diễn dịch mà có khi đến bằng sự mày mò, phép thử đúng sai, kinh nghiệm và dự đoán sắc sảo. Thật ra, kỷ năng dự đoán chính xác cũng là một trong những nhân tố chính yếu làm nên một nhà toán học có tầm cở. Điều quan trọng ở đây là người Hy lạp nhấn mạnh rằng những phát kiến toán học dự đoán hoặc tìm được qua thực nghiệm phải đi tiếp bằng phép chứng minh minh diễn dịch nghiêm nhặt mà không một lượng dù lớn đến đâu của thực nghiệm có thể thay thế được.

Để thành công trong hình học, dù là một nhà sáng tạo hoặc đơn giản là người giải toán, ta cũng phải sẵn sàng thí nghiệm, vẽ hình và kiểm tra nhiều trường hợp, thử hướng này, thử hướng nọ. Galileo (1564 – 1642), đã cố gắng tính diện tích giới hạn bởi một đường cycloid sinh bởi một đường tròn khi lăn trên một đường thẳng (Hình dưới). Sau những suy tư bằng vật lí qua khái niệm trọng tâm, ông ta cho rằng, và điều này sai, diện tích đó gần bằng nhưng không bằng đúng ba lần diện tích của hình tròn.

Việc chứng minh diện tích đó thật ra bằng đúng ba lần diện tích hình tròn đã được công bố lần đầu tiên vào năm 1644 bởi học trò của ông, Torricelli (1608-1647), bằng cách dùng phương pháp tích phân.

Blaise Pascal (1623 – 1662), khi còn là một thiếu niên, đã phát hiện tổng số góc trong một tam giác bằng một góc bẹt nhờ thí nghiệm xếp hình tam giác bằng giấy.

Archimedes(287? – 212 TCN), trong chuyên luận Phương Pháp của ông, đã kể ông đã làm thế nào, bằng phương pháp cơ học, tìm ra được công thức thể tích khối cầu là 4πr³ /3, trong đó r là bán kính khối cầu. Nhưng lương tri toán học của ông không cho phép ông công nhận kết quả này là một chứng minh, và sau đó ông đã tìm cách chứng minh công thức một cách nghiêm chỉnh.

Bằng cách xây dựng một khối nón tròn xoay, đổ đầy khối với cát ba lần, rồi lấy số cát ấy đổ vào khối trụ tròn xoay có cùng chiều cao và bán kính đáy với khối nón, ta có thể dự đoán rằng thể tích khối nón bằng một phần ba tích số chiều cao và diện tích đáy.

Người ta không nên đánh giá thấp phương pháp thực nghiệm và những lối tiếp cận dạng này, vì không nghi ngờ gì nữa nhiều kết quả hình học đã được phát hiện bởi phương pháp này. Lẽ dĩ nhiên, một khi một dự đoán hình học đã được thiết lập, người ta phải, theo gương Archimedes, dùng lí luận diễn dịch để chứng minh nó đúng hoặc nó sai, và như thế mớí là cách giải quyết rốt ráo vấn đề. Nhiều ức đoán hình học đã được loại bỏ chỉ sau khi một hình được vẽ kỹ lưỡng hoặc sau khi xét một trường hợp đặc biệt.

Một cách màu mỡ giúp tìm ra những dự đoán hình học là sử dụng phương pháp tương tự, mặc dù phải công nhận rằng nhiều dự đoán theo cách ấy cuối cùng cũng sai. Một số lượng đáng kinh ngạc của hình học không gian cũng đã được dự kiến qua sự tương tự hoá các kết quả đã biết trong hình học phẳng.

Có một nguyên tắc sư phạm dựa trên một định luật nổi tiếng trong sinh học dưới dạng “sự phát sinh cá thể tóm lược sự phát sinh loài”, tức nóí một cách đơn giản là : “cá thể lặp lại sự phát triển của cả nhóm”. Nguyên tắc sư phạm là, ít nhất về đại thể, một sinh viên nên được dạy một môn học nào đó theo đúng trình tự mà môn học ấy đã phát triển qua thời gian. Lấy hình học làm ví dụ, chẳng hạn. Chúng ta đã biết rằng theo lịch sử, hình học phát triển theo ba giai đoạn – đầu tiên là hình học trực giác, sau đó hình học thực nghiệm và cuối cùng là hình học chứng minh. Nguyên tắc sư phạm tuyên bố rằng loại hình học đầu tiên nên dạy cho trẻ nhỏ là hình học trực giác, chắc chắn là qua những hình vẽ nghệ thuật đơn giản và việc quan sát thế giới tự nhiên. Trong giai đoạn này, các học sinh nhỏ tuổi sẽ vô tình nhận ra được nhiều khái niện cơ bản của hình học như khoảng cách, góc, tam giác, tứ giác, tính vuông góc, song song, đường thẳng, đường tròn, hình cầu, hình trụ, hình nón. . . Rồi dần dần những căn bản trực giác này sẽ tiến hoá thành loại hình học thực nghiệm, trong đó học sinh sẽ tìm được những dữ kiện hình học bằng các phương pháp thực nghiệm với công cụ thước kẻ, compa, thước đo độ. . . dùng kéo cắt dán các mô hình đơn giản như trong thủ công. Rồi tiếp theo, khi học sinh đã đủ chín mùi về nhận thức, hình học chứng minh mới được đưa vào, và những điều tiện lợi hay bất cập của phương pháp tiếp cận đã biết trước đây sẽ được chỉ ra.

Điểm yếu nhất trong chương trình hình học của chúng ta hiện nay hình như là ở giai đoạn hai, giai đoạn thực nghiệm hình học. Quá ít thời gian dành cho giai đoạn này. Đáng lí ra phải dành cho học sinh nhiều thời gian hơn để chúng nắm bắt được sâu sắc những khái niện hình học cơ bản. Ở đây chúng cũng nhận ra được sự quan trọng của phương pháp qui nạp sơ khởi trong toán học, đồng thời được chỉ ra những bất cập của nó nêu không được chứng minh một cách nghiêm túc bằng phương pháp diễn dịch. Điều các thầy giáo cần khi dạy loại hình học của giai đoạn này là một tập hợp những thí nghiệm hình học đơn giản sử dụng các mô hình dễ làm và rẽ tiền. Chắc chắn kết quả là sự hứng thú toán học của học sinh sẽ được khơi dậy, và đó là một đền bù xứng đáng cho công lao đầu tư của các nhà gõ đầu trẻ trong hướng đi mới mẻ và đầy sáng tạo này.