Nghiên Cứu Lịch Sử

15. Trật tự trong sự hỗn loạn

 Howard Eves

Trần Quang Nghĩa lược dịch

 Trong những loại xương cấu tạo nên bộ khung xương phức tạp và tinh vi của bàn chân là phần xương nằm trong gót chân ngay phía trên xương talus, gọi là xương sên. Ở loài người hoặc các động vật cao cấp có xương bàn chân phát triển, xương sên có hình dạng hoàn toàn không đều đặn, nhưng trong loài có móng, như trừu, dê, hươu nai, xương sên có hình hơi đối xứng, tiết diện gần như vuông với hai đầu bo tròn, một đầu hơi lồi, đầu kia hơi lõm. Những phần xương này đặc chắc và không có tủy, cứng và bền chắc, dáng dấp có hình khối với các rìa kích thước khoảng hai phân hoặc ít hơn, có thể đánh bóng lên.

Đối với các nhà khảo cổ khai quật các di tích tiền sử, thông thường người ta hay tìm gặp một bộ sưu tập đáng kể các loại xương sên của loài động vật có móng, và đôi khi có một số hòn đá nhỏ có màu sắc khác nhau. Hình như có lý khi ức đoán rằng những mảnh xương và những hòn đá sỏi này có thể đã được các người tiền sử dùng để khắc ghi, đánh dấu các số đếm, và cũng có thể là các đồ chơi cho con cháu họ (Hình dưới).

Trong khi cách sử dụng xương sên như đã nói trên trong quần thể các người tiền sử chỉ là ức đoán, thì việc những người Babylon và Ai cập, người Hi lạp và La mã thời trước Công nguyên, dùng xương sên để làm đồ chơi cho trẻ em là điều chắc chắn.   Chúng ta biết rằng những học sinh chơi với chúng mọi lúc, mọi nơi, thình thoảng giữ cân bằng 4 khúc xương sên trên các khớp ngón tay, rồi dùng ngón tay vẩy chúng lên không và rồi cố bắt lại khi chúng rơi xuống. Cũng vậy, quan sát các bức vẽ trên bình hoa, người ta thấy các khúc xương sên thường được ném vào trong một vòng tròn vẽ trên mặt đất, giống như ngày nay các em chơi bắn bi. Từ triều đại đầu tiên ở Ai cập (khoảng 3500 trước Công nguyên), xương sên được dùng trong nhiều trò chơi. Các trẻ em ngày nay ở Pháp và Ý vẫn còn chơi những trò với xương sên, và lẽ dĩ nhiên xương sên được thay bằng các thẻ kim loại, có thể mua ở các tiệm trong làng.

Có phải trò cờ bạc phát triển từ trò chơi, hay từ việc đánh cá và rút thăm, hay từ việc bói toán và chiêm tinh hoặc sấm truyền? Trong bất cứ trường hợp nào, khoảng 1200 TCN , hột xúc sắc đã tiến hoá thành một nhân tố tạo ngẫu nhiên thích hợp hơn là ném khúc xương sên. Nó đã xuất hiện đồng thời tại nhiều phần khác nhau trên thế giới, và điều chắc chắn rằng hột xúc sắc đầu tiên được làm bằng cách chà trẹt hai mặt tròn đối diện nhau của xương sên. Các mặt của hột được đánh dấu sau đó bằng cách khoan các vết lõm tròn từ 1 đến 6.

Trò cờ bạc gắn với hột xúc sắc đơn giản và tự nhiên nhất chắc chắn bắt đầu bằng cách ném hột, và người chơi chỉ chú ý đến may rủi hay xác suất khi tính tổng các mặt số hiện lên khi ném một hay nhiều hột. Do đó, mặc dù các nhà triết lí Hi lạp thời cổ cũng bàn luận đôi chút về quy luật tất yếu và tính ngẫu nhiên, nhưng đúng ra là chính những nỗ lực tính toán độ may rủi trong trò đánh bạc chính là nguồn gốc của phép tính xác suất.

Thật khó cho các nhà toán sử giải tích sự ra đời chậm trể của môn tính xác suất. Có lẽ là phải đợi cho đến khi một hột xúc sắc “vô tư” ra đời, nghĩa là hột súc xắc mà sự xuất hiện 6 mặt đều có cơ hội xảy ra như nhau, chứ ném một cái xương sên lõng thõng hay một miếng gỗ hoặc ngà thì độ xác suất của các mặt không thể tính được.

Chúng ta biết rằng các vua La mã cũng như giai cấp giàu có đều mê đánh bạc. Chẳng hạn vua Claudius (10 TCN – 54 CN) giành nhiều thì giờ đổ hột xúc sắc và còn viết một cuốn sách tựa là Làm Thế Nào Để Thắng Khi Đổ Hột, rất tiếc đã thất truyền. Nhưng sự khai sinh của môn khoa học tính độ ngẫu nhiên không xảy ra cho đến thời Phục Hưng, khi khả năng viết và tính số đã lưu truyền rộng rãi, và đại số học cơ bản đã phát triển.

Nhưng mãi đến cuối thế kỉ thứ 15 và đầu thế lỉ 16 mới bắt đầu có những nghiên cứu toán học thực sự về khoa học xác suất, khi có một số nhà toán học Ý cố gắng tính độ may rủi trong một số trò chơi, trong đó có trò đổ hột. Cardano (1501-1576), như ta đã gặp trong bài 16, có viết một cẩm nang ngắn trong đó một số dáng dấp đơn giản của xác suất toán học được đề cập. Nhưng hầu hết mỗi người đều công nhận rằng một bài toán có thê được vinh danh là nguồn cội của khoa học xác suất là bài toán gọi là bài toán tính điểm. Bài toán yêu cầu xác định phần chia tiền đặt cược khi ngừng một cuộc chơi may rủi giữa hai người chơi được giả sử là ngang tài nhau, cho biết số điểm của mổi người tại thời điểm dừng cuộc chơi và số điểm cần thiết để thắng cuộc chơi. Huynh Luca Pacioli (1445-1509), trong quyển Suma phổ thông của ông, là một trong các tác giả đầu tiên giới thiệu bài toán tính điểm trong một tác phẩm toán học. Bài toán sau đó được Cardano và Tartaglia tham gia. Tất cả họ đều đi tới những kết luận không đúng đắn.

Một sự tiến bộ thực sự chỉ xảy ra khi bài toán được đưa đến Pascal vào năm 1654 từ tay ngài Méré, một tay đánh bạc nhiều kinh nghiệm và có năng lực. Ông nhờ tài năng của Pascal vì ông nhận thấy suy luận và tính toán của mình về bài toán không phù hợp với thực tế. Pascal tỏ ra quan tâm với bài toán và trao đổi thư từ với Fermat. Từ đó bắt đầu một cuộc trao đổi thư tín giữa hai nhà toán học trong đó mỗi người có cách giải bài toán khác nhau và cùng là cách giải đúng. Chính qua cuộc trao đổi thư từ này mà Pascal và Fermat đều là các đồng sáng lập ngành toán học về lý thuyết xác suất đáng được vinh danh, đánh dấu MỘT THỜI KHẮC TRỌNG ĐẠI CỦA TOÁN HỌC.

Pascal

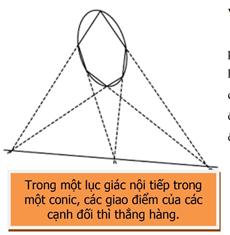
Pascal sinh năm 1623 trong miền Auvergne của Pháp và từ bé đã bộc lộ một năng khiếu toán học phi thường. Khi chỉ 12 tuổi, hoàn toàn tự học, ông đã khám phá nhiều định lí hình sơ cấp. Lúc 14 tuổi, ông đã là thành viên trong một nhóm các nhà toán học gặp gỡ nhau hằng tuần, và sau này, năm 1666, trở thành Viện Hàn Lâm Pháp. Năm 16 tuổi, ông đã khám phá, trong nhiều thành tựu, định lí về “lục giác thần bí” phong phú khác thường trong môn hình học họa hình. Vài năm sau, ông sáng chế ra máy tính cộng đầu tiên và bắt đầu áp dụng tài năng kiệt xuất vào lĩnh vực vật lí và cơ học. Năm 1648, ông trước tác một toán luận súc tích về hình học họa hình, nhưng đã thất lạc.

Hoạt động của một tài năng sớm phát triển và xuất phàm này đã ngừng lại thình lình vào năm 1650, khi, vì sức khoẻ kém, Pascal quyết định từ bỏ toán học và khoa học để chuyên tâm vào các suy nghiệm tôn giáo. Ba năm sau, tuy vậy ông trở lại toán học trong một thời gian ngắn ngủi, trong đó ông viết cuốn Traité du triangle arithmétique (Luận về tam giác số học), mà chúng ta sẽ thấy sau đây, đóng một vai trò quan trọng trong môn xác suất mà ta đang bàn đến.

Ông tiến hành nhiều thí nghiệm về áp suất của chất lỏng, đưa đến phát minh về sức ép thủy lực, và đơn vị áp suất được mang tên ông. Rồi đến năm 1654, bắt đầu cuộc trao đổi thư từ lịch sử để hình thành lý thuyết và toán xác suất.

Vào cuối năm 1654, sau một tai nạn khi chiếc xe song mã đâm sầm vào thành cầu đá giết chết cả hai con ngựa ngay tại chỗ, ông bị thương nặng nơi ngực, và thoát chết trong gang tấc. Pascal nghĩ rằng mình đã nhận được một mặc khải từ Thượng Đế, phán rằng việc ông quay trở lại toán học và khoa học đã làm Ngài phật ý. Ông ngoan ngoản trở về với thần học.

Chỉ một lần duy nhất nữa là vào năm 1685, Pascal trở lại với toán. Đó là dạo ông đang bị nhức răng kinh khủng, một ý tưởng hình học lóe lên trong đầu, và chiếc răng đang đau bổng ngừng hành hạ ông. Cho rằng đây là ý Chúa, ông dùi đầu tám ngày liền vào toán để phát triển ý tưởng vừa manh nha, và một tiểu luận về đường cycloid ra đời.

Những Lá Thư Thôn Quê và Tư Tưởng là các tác phẩm nổi tiếng của Pascal, bàn về các vấn đề tôn giáo được ông viết vào những ngày cuối của cuộc đời ngắn ngủi của mình, ngày nay được coi là kiểu mẫu của văn chương cổ điển Pháp. Ông mất tại Paris sau một cơn bạo bệnh kéo dài vào năm 1662 ở tuổi 37 non yểu.

Trái với cuộc đời ngắn ngủi, dày vò và luôn thống khổ vì các cơn hoang tưởng tôn giáo của Passal, cuộc đời của Fermat tương đối dài, bình an, sung mãn và hầu như hoạt động liên tục. Ông sinh ở Beaumont de Lomagne gần Toulouse của Pháp, vào năm 1601(?), con một thương gia giàu có, lúc nhỏ cũng học ở nhà như Pascal.

Fermat

Năm 1631, Fermat lập nghiệp tại Toulouse với chức danh ủy viên hội đồng thanh tra, và năm 1648 được đề bạt đến chức cố vấn Nhà vua tại nghị viện địa phương. Trong chức vụ này, ông làm tròn trách nhiệm với sự cẩn trọng và tỉ mỉ của một luật sư về hưu nhún nhường, và dành trọn thời gian rảnh rỗi để nghiên cứu và sáng tạo toán học. Mặc dù lúc sinh thời ông ít khi xuất bản công trình nghiên cứu của mình, ông lại thường trao đổi thư từ khoa học với nhiều nhà toán học hàng đầu của thời đại, và do đó có ảnh hưởng rất nhiều với người đương thời.

Fermat đã làm giàu cho nhiều ngành toán học với nhiều đóng góp quan trọng, được đánh giá là nhà toán học Pháp vĩ đại nhất của thế kỉ 17. Trong bài trước, chúng ta được biết ông là đồng sáng lập ngành hình giải tích, trong bài này chúng ta sẽ biết đến ông như người đặt nền tảng cho lý thuyết xác suất, và trong bài sau chúng ta sẽ thấy phần đóng góp của ông vào sự phát triển khởi thủy của môn vi tích phân cũng rất đáng kể. Nhưng trong những đóng góp khác nhau của ông cho toán học, đóng góp nổi bật nhất là sự xây dựng lý thuyết số hiện đại, một ngành toán học trong đó ông bộc lộ một năng khiếu phi thường và một năng lực ấn tượng và đáng kinh ngạc, đặt ông lên tầm những nhà lý thuyết số hàng đầu của mọi thời.

Fermat mất tại Castres đột ngột năm 1665. Mộ ông, lúc đầu đặt tại Nhà Thờ Augustines ở Toulouse, sau đó đã được dời đến bảo tàng địa phương.

Chúng ta hãy trở về bài toán chia điểm, tìm hiểu cách giải của Fermat và Pascal trong thư từ trao đổi của họ năm 1654, bắt đầu một nghiên cứu nghiêm túc về xác suất.

Trường hợp minh họa bởi hai nhà toán học Pháp là trong đó ta tìm cách chia tiền đặt cược trong trò chơi giữa hai đối thủ ngang tài A và B khi đó A đang cần thêm 2 điểm nữa để thắng còn B cần thêm 3 điểm nửa để thắng. Trước tiên chúng ta sẽ xem cách giải của Fermat, cách này đơn giản hơn, cụ thể hơn; còn cách giải của Pascal thì tinh tế hơn và có thể tổng quát hoá được.

Dễ thấy rằng phải cần bốn lượt chơi nữa sẽ phân thắng bại. Fermat gọi a là lượt chơi mà A thắng điểm và b là lượt B thắng, có 16 hoán vị các khả năng có thể xảy ra là:

aaaa  aaab  abba  bbab

bbaa  bbaa  abab  babb

abaa  baba  aabb  abbb

 aaba  baab  bbba  bbbb

trong đó có 11 trường hợp A thắng 2 lượt trở lên và thắng cuộc chơi trong khi chỉ có 5 trường hợp B thắng 3 lượt trở lên và thắng cuộc chơi. Do đó tỉ lệ tiền đặt cược trong tình huống này phải được chia theo tỉ lệ là 11:5.

Trong trường hợp tổng quát, nếu A cần m điểm để thắng và B cần n điểm để thắng, hai người cần chơi 2^{m + n – 1} bàn để phân thắng bại. Ta liệt kê 2^{m + n – 1}  các hoán vị có thể xảy ra giữa hai chữ a và b lấy đúng m + n – 1 lần. Sau đó tìm số α các trường hợp trong đó a xuất hiện ít nhất m lần và đếm số β các trường hợp b xuất hiện ít nhất n lần. Tỉ lệ chia tiền đặt cược là α/β.

Pascal giải bài toán chia điểm bằng cách dùng “tam giác số học” (còn gọi là tam giác Pascal), một tam giác số gồm các dãy số đã được ông trình bày trong Traité du triangle arithmétique, mặc dù chỉ được in vào năm 1665, đã được ông viết từ năm 1653. Ông xây dựng “tam giác số học” của mình như trong hình 1. Bất cứ phần tử nào (từ hàng thứ hai trở xuống) đều là tổng của phần tử ở ngay trên nó và ở ngay bên trái số này. Ví dụ: 6 = 3 + 3 (chữ số màu nâu); hay 15 = 5 + 10 (chữ số xanh).

1    1

1    2    1

1    3    3    1

1    4    6    4    1

1    5   10  10   5    1

1    6   15  20  15   6    1

1    7   21  35  35   21   7    1

Các học sinh 12 có thể nhận ra là các số hạng của hàng số thứ n là hệ số liên tiếp trong khai triển (a + b)ⁿ  (gọi là nhị thức Newton). Ví dụ, các số ở hàng 4 là 1, 4, 6, 4, 1 là các hệ số của khai triển (a + b)⁴, tức là:

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

Pascal cũng dùng tam giác này để tìm số tổ hợp n chập r vật thể. Nhớ rằng một tổ hợp n chập r là một tập con gồm r vật thể lấy ra trong số n vật thể khác nhau. Ví dụ mỗi cách chọn ra một nhóm 3 người lấy trong số 5 người là một tổ hợp 5 chập 3.

Có thể tạo ra bao nhiêu nhóm tổ hợp n chập r? Pascal tìm ra số đó, kí hiệu C(n,r), là:

C(n, r) = n!/r!(n – r)!  trong đó

n! = n(n – 1)(n – 2). ..(3)(2)(1).

Chú ý C(n,0) = C(n,n) = n.

Ví dụ, có C(5,3) cách chọn nhóm 3 người từ một tập thể 5 người và:

C(5,3) = 5!/3!2!

           = 5.4.3.2.1/(3.2.1)(2.1)

           = 120/6.2 = 10

Trở lại bài toán chia tiền ban đầu, vì phải chơi 2 + 3 – 1 = 4 ván, nên xảy ra ta tất cả 2⁴ = 16 tình huống. Số tình huống a thắng cả 4 lần là C4,4) = 1, thắng 3 lần là C(4,3) = 4, thắng 2 lần là C(4,2) = 6. Do đó số tình huống a thắng 2 lần trở lên là: 1 + 4 + 6 = 11.

Tương tự, số tình huống b thắng 3 lần trở lên là:

C(4,4) + C(4,3) = 1 + 4 = 5.

Suy ra tỉ lệ chia tiền là 11:5.

Có nhiều hệ thức giữa những số của tam giác số học, một số này được phát hiện bởi Pascal. Pascal không phải là người đầu tiên tạo ra tam giác số học. Tam giác loại này đã được người Trung hoa và Ba tư biết đến vài thế kỉ trước. Nhưng vì nhiều tính chất của tam giác đã được Pascal tìm ra và áp dụng chúng nên tam giác này thường được gọi la tam giác Pascal. Qua tiểu luận của Pascal về tam giác, ông đã trình bày lần đầu tiên phương pháp quy nạp toán học.

Với việc giải bài toán chia điểm mà Fermat và Pascal đã trao đổi qua thư tín, MỘT THỜI KHẮC TRỌNG ĐẠI CỦA TOÁN HỌC được vinh danh và một lý thuyết toán học mới về xác suất đã vào bệ phóng. Năm 1657, một thiên tài toán học Hà lan tên Christiaan Huygens (1629-1695) viết một chuyên luận về xác suất, dựa vào các thư tín của Pascal-Fermat. Tiếp theo là di cảo của Jacob Bernouilli xuất hiện năm 1713, phát triển các công trình của Huygens lên một tầm cao mới. Sau những nổ lực tiên phong này, chủ đề xác suất được nhiều tài năng như De Moivre, Daniel Bernouilli, Leonard Euler, Louis Lagrange, Laplace, và còn nhiều nhiều nữa tham gia và phát triển.

Thật là mê hoặc và đồng thời cũng phần nào đáng kinh ngạc khi nhận ra rằng các nhà toán học có thể phát triển một ngành toán học trong đó các qui luật có lý có thể vận dụng vào những tình huống chỉ dựa vào yếu tố may rủi. Ngành khoa học này lại rất thực tế, nó là nền tảng của ngành thống kê, ngôn ngữ của mọi nghiên cứu, nó đã xâm nhập vào các ngành xã hội, sinh học, giáo dục, kinh tế, quản lý doanh nghiệp, giá trị của nó đã được chứng thực qua sự tồn tại của vô số công ty bảo hiểm lừng danh, Về ngành khoa học xác suất này, nhà toán học Pháp nổi tiếng Laplace nhận xét rằng, mặc dù nó bắt đầu bằng một vài nhận định trong các trò chơi may rủi tầm thường  nó đã trở thành một trong những lĩnh vực quan trọng nhất của kiến thức nhân loại. Còn nhà lí luận và kinh tế William Stanley Jevons (1835-1882) cho rằng nó là “một kim chỉ nam của cuộc sống và ít khi nào chúng ta đi một bước hoặc lấy một quyết định mà không làm một phép tính đúng hay sai về xác suất.”