Nghiên Cứu Lịch Sử

8 . Cú hích của Thiên Văn Học

 Howard Eves

Trần Quang Nghĩa lược dịch

 Sự khởi thủy môn lượng giác thì mơ hồ. Vào thời gian trước nền văn minh Hy lạp, trong các bản thảo bằng giấy dó ở vùng Rhind (khoảng 1650 TCN) có chứa những bài toán liên quan đến cotang của một góc nhị diện tạo bởi mặt bên và đáy của một hình chóp đều. Ngoài ra cũng có những bản đất sét hình nêm gọi là bảng Plimpton 322 (1900 đến 1600 TCN) có chứa một bảng tính 1/cosin của mười lăm góc từ 45^o đến 30^o. Đi sâu vào các nghiên cứu những di sản toán học của Mesopotamia cổ đại sẽ phát hiện một phát triển đáng kể của lượng giác học thực hành. Các nhà thiên văn học Babylon đã thu thập một lượng đáng kể những dữ kiện quan sát, và nhiều tư liệu này đã truyền lại cho người Hy Lạp. Chính từ nền thiên văn sơ khai này đã ra đời môn lượng giác cầu.

Một trong những nhà thiên văn Hy Lạp đầu tiên là Aristarchus thành Samos (310-230 TCN) được cho là đã vận dụng toán học vào thiên văn và là người đầu tiên đưa ra thuyết thái dương hệ. Không có công trình nào của ông được lưu truyền đến tay chúng ta, nhưng người ta cho rằng, trong công trình Về Kích Thước và Khoảng Cách Mặt Trời Và Mặt Trăng, ông đã sử dụng bất đẳng thức sau:

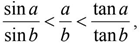
 trong đó 0 < b < a < π/2.

Nhà toán học-thiên văn học của Hy Lạp thời cổ nổi tiếng tiếp theo là Hipparchus, sinh tại Nicaea của Tiểu Á. Mặc dù ông đã thông báo một quan sát xuân phân ở Alexandria năm 146 TCN, những quan sát thiên văn quan trọng nhất của ông được thực hiện tại đài quan sát ở Rhodes. Nổi danh là người quan sát chính xác và tỉ mỉ, ông được vinh danh với nhiều thành tựu như xác định được tuần trăng trung bình chỉ sai 1 giây so với đo lường hiện đại, tính toán được chính xác độ nghiêng của quỹ đạo trái đất và xác định được cận điểm của mặt trăng, và đã liệt kê đến 850 định tinh.

Ông cũng khuyến cáo việc sử dụng vĩ độ và kinh độ để xác định vị trí trên mặt địa cầu. Và có thể ông là người đầu tiên chia đường tròn ra làm 360^o. Mặc dù sự hiểu biết của chúng ta về những công trình này chỉ là qua các tài liệu trung gian – vì không có tác phẩm nào của Hipparchus còn lưu truyền lại – chúng ta có thể nghĩ rằng Hipparchus đã nắm vững về lượng giác cầu cơ bản.

Một liên hệ trực tiếp hơn và rất quan trọng đến lượng giác của Hipparchus là qua lời trích dẫn của Theon thành Alexandria thế kỉ thứ 4 giới thiệu một bộ 12 quyển của Hipparchus về cách lập ra bảng lượng giác. Bảng này đã mất tích nhưng một quyển tiếp theo do Claudius Ptolemy (85 – 165) được cho là biên tập từ Hipparchus còn lưu lại. Bảng lượng giác Ptolemy cho độ dài các dây cung trương góc ở tâm của một đường tròn cho trước từ 1/2 độ đến 180 độ, cách nhau từng nửa độ một. Bán kính đường tròn được chia thành 60 phần bằng nhau và chiều dài của dây cung được tính theo các phần nhỏ này theo hệ lục thập phân. Nếu dùng kí hiệu crdα để chỉ độ dài của dây cung trương góc α, ta tìm thấy trong bảng đó số liệu sau:

crd 36^o = 37^p 4′ 55″

có nghĩa là độ dài dây cung của góc ở tâm 36^o bằng 37/60 bán kính (hoặc 37 phần nhỏ), cộng thêm 4/60 của một phần nhỏ, và thêm 55/360 của một phần nhỏ này.

Theo hình trên, bảng độ dài dây cung này tương đương với bảng tính sin lượng giác, vì:
    

Do đó bảng của Ptolemy thực tế là cho ta giá trị của sin những góc từ 0^o đến 90^o, cách nhau 1/4 độ.

Có tài liệu cho rằng Hipparchus đã dùng bảng của ông và hiển nhiên biết vài công thức hiện giờ được dùng để giải các tam giác cầu.

Theon cũng đề cập đến một công trình 6 quyển về dây cung đường tròn do Menelaus của Alexandria soạn ra (khoảng 100), nhưng trước tác này cũng thất truyền. Tuy nhiên còn công trình ba quyển của Menelaus có tên là Sphaerica, còn lưu lại bằng tiếng Ả rập. Tác phẩm này cho ta thấy được mức phát triển của môn lượng giác Hy Lạp.

Sự kiện có quá nhiều công trình thiên văn Hy Lạp sơ khai đã biến mất nguyên nhân là do tác phẩm của Ptolemy quá xuất sắc đã khiến chúng bị lu mờ và chìm vào quên lãng. Đó là quyển Tuyển Tập Toán Học, viết vào khoảng năm 150, một công trình thiên văn đầy đủ, súc tích và đẹp đẽ. Để phân biệt tác phẩm này với các công trình tầm thường khiêm tốn hơn, các nhà toán sử thêm vào tên tác phẩm từ magisse (vĩ đại nhất).    Về sau, những nhà phiên dịch Ả rập còn thêm tiếp đầu ngữ al, và vì thế tác phẩm này có tên Almagest. Bộ sách gồm 13 quyển và trong quyển I, ngoài những dữ liệu thiên văn cơ bản, còn có bảng số độ dài dây cung đã nói ở trên, và phần giải thích cách lập bảng số từ một công thức nổi tiếng mang tên ông, định lí Ptolemy: Trong một tứ giác nội tiếp được trong đường tròn, tích hai đường chéo bằng tổng tích hai cặp cạnh đối.

Chắc chắn lượng giác học thực hành sẽ không tiến bộ nhiều nếu không có bảng số lượng giác. Cách lập bảng lượng giác một cách đầy đủ và có hệ thống do đó đánh dấu MỘT THỜI KHẮC TRỌNG ĐẠI CỦA TOÁN HỌC.

Công việc tiếp theo trong bài này là theo dõi phương pháp mà Ptolemy dùng để lập ra bảng sin nói trên. Để tiện, ta dùng phân số để diển đạt độ dài thay vì dùng hệ lục thập phân như Ptolemy đã dùng. Và ta trình bày từng bước tính một như sau:

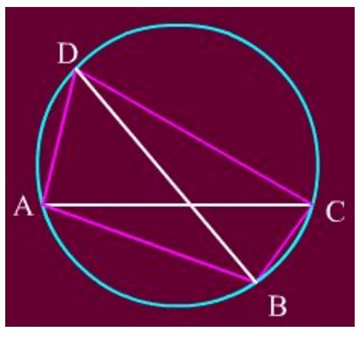
1. Ta đã biết cách chứng minh định lí Ptolemy trong một tứ giác nội tiếp ABCD:

AC. BD = AB.CD + AD. BC.

Tiếp theo ta thiết lập ba hệ quả :

2. Hệ quả 1: Nếu a và b là hai dây cung của đường tròn bán kính đơn vị, thế thì :

    s = (a/2)(4 – b²)^1/2 +

                         (b/2)(4 – a²)^½

trong đó s là độ dài của dây cung của tổng hai cung (Hình trên phía  trên)

CM: Áp dụng định lí Ptolemy cho tứ giác ABCD trong đó AC là đường kính, BC = a và CD = b.

3. Hệ quả 2: Nếu a và b, a > b, là hai dây cung của đường tròn bán kính đơn vị , thế thì :

d = (a/2)(4 – b²)^1/2 – (b/2)(4 – a²)^1/2

trong đó d là độ dài của dây cung của hiệu hai cung.

CM: Áp dụng định lí Ptolemy cho tứ giác ABCD trong hình trên (dưới) với AB là đường kính, BD = a và BC = b.

4. Hệ quả 3: Nếu t là độ dài dây cung nhỏ và h là độ dài dây cung của nửa cung nhỏ đó trong đường tròn bán kính đơn vị, thế thì:

        h = [2 – (4 – t²)^1/2]^½

(Hình dưới)

CM: Áp dụng định lí Ptolemy cho tứ giác ABCD  với AC là đường kính, BD = t và BD vuông góc với AC. Ta được :

        2t = 2h(4 – h²)^1/2

Bình phương hai vế và thu gọn, ta được : h⁴ – 4h² + t² = 0

Giải phương trình này, và lấy nghiệm nhỏ vì h là độ dài dây cung nhỏ, ta được :

       h² = 2 – (4 – t²)^1/2

5. Xét tam giác cân AOB với góc đỉnh AOB = 36^o. Kẻ phân giác AC của góc A. Hai tam giác AOB và BAC đồng dạng cho ta:

       AB/CB = OB/AB

Đặt AB = x và cho OB = 1, ta có :

        x /(1 – x) = 1/x

<=> x² + x – 1 = 0

<=>   = 0, 6180 (lấy 4 chữ số thập phân). Đây chính là tỉ số vàng ta đã gặp ở bài 5.

Vậy trong đường tròn bán kính 1, ta có: crd 36^o = 0,6180.

6. Vì trong đường tròn đơn vị, crd 60^o = 1, dùng hệ quả 2, ta được: crd 24^o = crd(60^o – 36^o) = 0, 4158
7. Áp dụng hệ quả 3, ta có thể tính độ dài dây cung của 12^o, 6^o, 3^o, 90′, và 45′, được : crd 90′ = 0,0262, crd 45′ = 0.0131.
8. Theo bất đẳng thức :

      
với b < a < 90^o

mà ta đã trình bày ở đầu bài, đã được Aristarchus biết đến, cho ta :

   crd 60’/crd45′ < 60/45 = 4/3

hay crd 1^o < (4/3)(0,0131) = 0, 01747

Cũng thế :

crd 90’/crd 60′ < 90/60 = 3/2

hay crd 1^o > (2/3)(0,0262) = 0, 01747

Từ đó suy ra giá trị gần đúng đến 4 chữ số thập phân của crd 1^o = 0, 0175.

9. Dùng hệ quả 3, ta có thể tính được crd 1/2^o.
10. Và như thế chúng ta có thể thiết lập bảng độ dài dây cung của đường tròn đơn vị từng 1/2 độ một.

Nhiều công trình về sau của lượng giác thực hành là lập những bảng số càng ngày càng tốt hơn. Như nhà toán học Hồi Giáo Abul-wefa (940-998) đã lập bảng sin và tan từng 15 phút một. Sau đó một bảng sin đã được nhà toán học thành Vienna là Georg von Peurbach (1423-1461) lập và bảng tan do nhà toán học Đức Jahan Muller (1436-1476). George Joachim Rhaeticus (1514-1576), nhà thiên văn toán hàng đầu của thế kỉ 16, bỏ ra 12 năm, mướn các thợ tính toán, đã lập ra hai bảng tính lượng giác nổi tiếng vẫn còn hữu dụng. Một bảng tính gồm 10 chữ số thập phân các giá trị của sáu hàm lượng giác, cách nhau từng 10″ một, và bảng giá trị sin gồm 15 chữ số thập phân.

Cũng cần nhắc lại là Ban Tư Vấn Toán Học của Mỹ đã nhất trí quyết định hủy bỏ bảng số lượng giác khỏi Cẩm Nang Toán Học CRC nổi tiếng trong lần tái bản thứ năm. Sự ra đời của máy tính bỏ túi và sự lưu hành rộng rãi của nó đã khai tử bảng lượng giác có tuổi thọ hơn một ngàn tuổi.