Những Thời Khắc Trọng Đại của TOÁN HỌC- Bài 5

5. Lao đến khủng hoảng đầu tiên

Howard Eves

Trần Quang Nghĩa lược dịch

Những số nguyên chúng ta làm quen từ thuở niên thiếu được gọi là những số tự nhiên hoặc nguyên dương: 1, 2, 3, . . . Những số này là những khái niệm trừu tượng hình thành từ quá trình đếm tập hợp các vật thể hữu hạn. Về sau khi nhu cầu cuộc sống phát triển, đòi hỏi, ngoài việc đếm, chúng ta còn phải đo lường những đại lượng khác nhau như độ dài, trọng lượng, và thời gian. Để thỏa mãn những nhu cầu đo lường này, phân số đã được tạo ra, bởi vì ít khi, lấy ví dụ độ dài chẳng hạn, một kích thước nào đó đúng chính xác bằng bội số của đơn vị độ dài được chọn trước. Đối với vài đại lượng, như nhiệt độ thấp chẳng hạn, số zero và số nguyên âm và phân số âm tỏ ra tiện lợi. Hệ thống số của chúng ta dần dần được mở rộng. Nhưng, nếu chúng ta định nghĩa số hữu tỉ là thương của hai số nguyên, p/q với q khác 0, thì tập hợp các số hữu tỉ, vì chúng chứa luôn cả tập hợp các số nguyên, đã đủ dùng cho mọi mục đích đo lường thực tiễn của chúng ta.

Giờ đây những số hữu tỉ có được biểu diễn hình học như sau: Lấy 2 điểm phân biệt O và I trên đường thẳng, I ở bên phải của O, và chọn độ dài OI là đơn vị độ dài. Nếu chúng ta chọn O là điểm biểu diễn số 0, I là điểm biểu diễn số 1, thế thì những số nguyên dương và âm có thể biểu diễn bằng những điểm lần lượt ở bên phải và trái của O và cách nhau bằng đơn vị độ dài.

Số hữu tỉ có mẫu là q có thể được biểu diễn bằng những điểm chia các đoạn có độ dài là đơn vị ra thành q phần bằng nhau. Như thế với mỗi số hữu tỉ, ta có một điểm biểu diễn duy nhất trên trục số. Đối với các nhà toán học thời cổ, cũng như đa số chúng ta ngay thời nay, thật là hiển nhiên khi cho rằng mọi điểm trên đường thẳng đã được tận dụng để biểu thị mọi số hữu tỉ.

Đúng là một cứ sốc trí tuệ khi biết rằng còn nhiều điểm trên đường thẳng chưa dùng đến, thậm chí những điểm chưa dùng tới còn ” nhiều ” hơn số điểm đã được dùng để biểu diễn số hữu tỉ. Phát hiện này chắc chắn là một trong những thành tựu vĩ đại nhất của Hy Lạp Cổ Đại, và xảy ra trong khoảng thế kỉ thứ năm hoặc thứ sáu TCN trong hội kín huynh đệ Pythagoras. MỘT THỜI KHẮC TRỌNG ĐẠI CỦA TOÁN HỌC đã điểm.

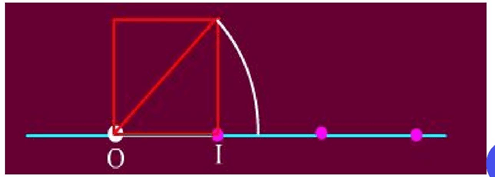
Cụ thể các hội viên Pythagoras đã phát hiện rằng không có số hữu tỉ nào tương ứng với điểm P trên trục số mà OP bằng độ dài đường chéo của hình vuông cạnh bằng đơn vị. Về sau, nhiều điểm trên trục số được tìm ra, cũng không tương ứng với số hữu tỉ nào. Những số mới phải được tạo ra để tương ứng với những điểm như thế, và vì chúng không phải là số hữu tỉ nên được gọi là những số vô tỉ.

Theo Pythagoras, độ dài đường chéo hình vuông cạnh đơn vị

là , ta sẽ chứng minh điểm P nói trên không phải là điểm biểu diễn số hữu tỉ, tức là chứng minh nó là số vô tỉ. Để chứng minh, trước hết nhận xét rằng với số nguyên dương s, s² là chẵn khi và chỉ khi s chẵn. Bây giờ giả sử là số hữu tỉ tức

= p/q,

trong đó p, và q là hai số nguyên tố cùng nhau (tức không có ước số chung khác 1)

Thế thì: p = q

<=> p² = 2q² (*)

Như vậy p² là số nguyên chẵn, suy ra p là số chẵn. Tức p = 2r, và (*) thành:

4r² = 2q² <=> 2r² = q²

Từ đó q² là số chẵn, và do đó q cũng là số chẵn. Nhưng điều này là vô lí vì như thế p và q không nguyên tố cùng nhau như đã giả sử. Vậy không thể là số hữu tỉ, tức là số vô tỉ.

Cách chứng minh này đã được Aristotle (384-322 TCN) công bố. Theo Plato (427-347 TCN), sau khi số đã được chứng minh là số vô tỉ, Theodorus (425 TCN) đã chứng tỏ các căn số bâc 2 của 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, cũng là số vô tỉ.

Cần chú ý là phép chứng minh trên đây gọi là phép phản chứng, một kết quả của lôgic học, cụ thể để chứng minh một mệnh đề nào là đúng mà ta không thể chứng minh một cách trực tiếp, ta giả sử nó sai. Bằng lập luận hợp lý, ta dẫn đến một mệnh đề vô lý, thường là trái với giả thiết hoăc trái với những điều đã được thiết lập là đúng. Chẳng hạn, cho dễ hiểu, để thuyết phục phát biểu “ai bị béo phì thì y sẽ bị bệnh tiểu đường,” ta có thể chỉ cho thấy “ai không bị tiểu đường thì y không phải là người béo phì.” Nhà toán học Anh G. H. Hardy (1877-1947) đã ví lối chứng minh này như là thế “cờ thí” trong nghệ thuật đánh cờ, trong đó cờ thủ hi sinh một quân cờ để được một thế áp đảo đối với đối phương.

Sự phát hiện số vô tỉ đã khuấy động một niềm tin dựa vào trực giác của Hy Lạp Cổ. Cho hai đoạn, tư duy thông thường mách bảo rằng phải có một đoạn thứ ba, có thể rất, rất nhỏ, dùng làm đơn vị sao cho cả hai độ dài cho trước đều bằng một số nguyên lần đơn vị ấy. Ngay cả bản thân chúng ta, nếu không được dạy trước, cũng hẳn đã nghĩ như vậy. Hãy lấy hai đoạn có độ dài s và d lần lượt là độ dài cạnh và đường chéo hình vuông. Bây giờ nếu tồn tại một đoạn thứ ba t có thể dùng để đo s và d theo các số đo nguyên, thế thì : s = qt và d = pt, trong đó p, q là các số nguyên dương. Nhưng d = s, suy ra :

pt = qt

Do đó p = q

hay = p/q, một số hữu tỉ. Như thế là vô lí, do đó, trái với trực giác thông thường, tồn tại những đoạn thẳng vô ước, đó là những đoạn thẳng không có đơn vị đo lường chung.

Ta trình bày cách chứng minh khác, bằng hình học, rằng là số vô tỉ, bằng cách chỉ ra rằng cạnh và đường chéo một hình vuông là những đoạn vô ước. Giả sử chúng hữu ước, thế thì tồn tại đoạn AP (xem hình trên) sao cho cạnh AB và đường chéo AC đều hữu ước đối với AP, tức độ dài AB và AC là bội số của độ dài AP. Trên AC lấy điểm B₁ sao cho CB₁ = CB và vẽ B₁C₁ vuông góc với CA. Dễ dàng chứng minh được:

C₁B = C₁B₁ = AB₁ = AC – BC

Thế thì AB₁ và AC₁ = AB – AB₁

đều hữu ước với AP. Nhưng AC₁ và AB₁ là cạnh và đường chéo một hình vuông có kích thước nhỏ hơn phân nửa của hình vuông ban đầu. Lập lại tiến trình này nhiều lần liên tiếp ta cuối cùng được một hình vuông có đường chéo AC_n và cạnh AB_n hữu ước với AP mà AC_n < AP. Điều này vô lí và định lí được chứng minh.

Thời cổ người Hy Lạp còn chạm trán với số vô tỉ khi tìm cách dựng một ngũ giác đều bằng thước và compa. Trước đây họ đã dựng được tam giác đều, tứ giác đều và sau đó dựng lục giác đều không mấy khó khăn. Nhưng dựng ngũ giác đều bằng thước và compa là một việc khác. Muốn dựng được, ta phải dựng được một góc bằng 36^o hay 72^o là góc ở tâm trương cạnh của ngũ giác đều nội tiếp trong đường tròn.

Nếu xét tam giác cân OAB có góc đáy là 72^o thì góc đỉnh sẽ là 36^o. Gọi AC là phân giác góc A, ta có: OC = AC = AB và hai tam giác OAB và ABC đồng dạng. Lấy OA = 1 và đặt AB = x, ta có:

AB/BC = OA/AB (*)

<=> x /(1 – x) = 1/x

<=> x² + x – 1 = 0 <=>

Cách dựng độ dài này là điều dễ dàng, như được chỉ ra trong hình trên với OA = 1, OM = 1/2 thì AM = /2 và AB = AN = AM – MN =

Suy ra dễ dàng các bước dựng tiếp theo của ngũ giác đều.

(*) có thể viết lại là:

CO/CB = 1/x =

điểm C như thế được gọi là điểm chia đoạn OB theo tỉ số vàng và tỉ số này hình như xuất hiện mọi nơi trong tự nhiên.

Chúng ta sẽ bàn đến sự xuất hiện của tỉ số này trong tự nhiên trong bài 15. Ở đây ta chỉ nhận xét một khuynh hướng tâm lí cho thấy rằng phần đông chúng ta đều nhìn hình chữ nhật mà chiều dài và chiều rộng có tỉ lệ vàng là hình chữ nhật bắt mắt nhất. Hình chữ nhật này được gọi là hình chữ nhật vàng. Tỉ lệ vàng và hình chữ nhật vàng đã được kiến trúc và đồ gốm Hy Lạp ưa chuộng, cũng như trong điêu khắc, hội họa, thiết kế nội thất . . .

Sự khác biết nền tảng giữa số hữu tỉ và vô tỉ được biểu hiện sinh động dưới dạng thập phân của chúng. Ta chứng minh được dễ dàng mọi số hữu tỉ đều được biểu diễn bằng khai triển thập phân hoặc hữu nhạn như 7/4 = 1,75 hoặc bằng một khai triển vô hạn trong đó có chứa một nhóm chữ số lặp lại tuần hoàn, như 47/22 = 2,1363636 . . . Nhóm chữ số lặp lại tuần hoàn vô hạn là 36, và số đó được kí hiệu: 2, 1 (36).

Ngược lại mọi khai triển có tính chất trên chính là một số hữu tỉ. Như vậy một số có khai triển thập phân vô hạn không tuần hoàn là một số vô tỉ, như số: 0,101001000100001. . . (các chữ số 0 tăng dần lên theo sau là chữ số 1 hay 0,123456789101112 . . . (các chữ số là những số nguyên dương liên tiếp) là những số vô tỉ.

Ta có thể tìm được số hữu tỉ mà khai triển của nó là một số thập phân vô hạn tuần hoàn cho trước bằng một thuật toán đơn giản của cấp 2. Ví dụ với số hữu tỷ r có khai triển 3,4251251251 . . . hay 3,4(251), ta viết

r = 3,4 + 0,0251251251 .

Đặt x = 0,0251251 . . .

Suy ra: 10000x = 251,251251 . . .

hay 1000x = 251 + 10x

hay 9990 x = 251

<=> x = 251/9990

Do đó: r = 3, 4 + 251/9990 =

= 34217/9990

Trong năm 1967, những nhà toán học Anh, dùng máy tính, đã tìm được khai triển thập phân của đến 100.000 chữ số. Trong 1971, Jacques Dutka của Đại học Columbia, sau 47,5 giờ tính bằng máy, đã tìm được đến 1.000.082 chữ số khai triển, chứa đến 200 trang giấy in, mỗi trang chứa đến 5000 chữ số. Ngày nay công việc buồn tẻ này thường được xem là bước chạy thử cho nóng máy mỗi lần một máy tính cực mạnh mới ra lò, và số các chữ số thập phân đã đến cả trăm triệu là điều bình thường.

Bạn có thể kết thúc bài này bằng cách chứng minh các tính chất sau: