Nghiên Cứu Lịch Sử

2. Kim tự tháp vĩ đại nhất của Ai cập

 Howard Eves

Trần Quang Nghĩa lược dịch

 Những nhận định hình học đầu tiên của con người phải có từ rất lâu, xuất phát một cách vô thức từ những quan sát và nhận ra những dạng hình và so sánh kích thước cũng như hình thể của chúng. Chắc chắn một trong những khái niệm xa xưa nhất mà con người có thể cảm nhận được là khái niệm vể khoảng cách, đặc biệt là phát hiện rằng đoạn thẳng là khoảng cách ngắn nhất nối hai điểm. Một khái niệm xa xưa nữa xuất hiện từ vô thức đến nhận thức là các dạng hình đa giác, như hình tam giác, tứ giác.   .   .  Thật là tự nhiên khi người ta vạch ra những đường biên bằng cách ấn định những điểm trên mặt đất rồi nối hai điểm liên tiếp bằng những bức tường thẳng hay hàng rào. Trong quá trình xây dựng các bức tường khái niệm thẳng đứng, song song, và vuông góc sẽ dần dần lộ diện. Nhiều đường cong đặc biệt nổi bật trên những đường phức tạp của thiên nhiên, sẽ dần dần gây ấn tượng lên tâm trí vô thức của con người. Chẳng hạn những đĩa tròn là hình ảnh của mặt trời, mặt trăng, hay đường cầu vòng hay mặt cắt các thân cây. Rồi quỹ đạo parabol của một viên đá ném đi, đường dây xích của dây nho buông thõng, đường xoắn ốc của dây thừng khi cuộn lại, của những tua các loài dây leo cũng gây chú ý cho các bộ óc ít quan sát nhất. Một số loài nhện giăng tơ theo những hình đa giác đều. Những dợn sóng là những đường tròn đồng tâm tỏa ra khi một hòn đá được ném xuống hồ, những đường xoắn ốc nghệ thuật trên vỏ các loài ốc biển. Nhiều quả có dạng khối cầu; thân cây thì hình trụ; những dạng hình nón xuất hiện đây đó trong tự nhiên. Những bề mặt và những khối tròn xoay, được quan sát trong tự nhiên cũng như trong sản phẩm của các thợ gốm, sẽ dần dần tác động một cách vô thức đến những trí óc hay tò mò. Con người, loài vật, và nhiều chiếc lá cũng có trục hay mặt đối xứng. Kháí niệm về thể tích thành hình mỗi lần một bình chứa được đổ đầy nước ở bờ suối hay bờ sông. Khái niệm về không gian và điểm trong không gian được liên kết mỗi lần nhìn lên bầu trời đầy sao ban đêm. Danh sách liệt kê như trên có thể kéo dài vô tận.

Việc làm quen ban đầu với những khái niệm hình học theo cách trên có thể được gọi là hình học vô thức. Những người tiền sử đã quen với cách này cũng như các trẻ em ngày nay thể hiện trong các bức vẽ của chúng.

Giai đoạn thứ hai trong hình học xuất hiện khi trí tuệ con người biết rút ra từ tập hợp những liên hệ hình học cụ thể một mối liên hệ trưù tượng tổng quát mà những liên hệ cụ thể nói trên chỉ là một trường hợp cá biệt. Bằng cách này người ta đã thiết lập được một qui tắc hình học. Ví dụ, bằng cách tính diện tích các hình chữ nhật trên các giấy ô vuông bằng cách đếm các ô vuông đơn vị mà chúng chứa đựng, một học sinh tiểu học có thể rút ra qui tắc tính diện tích hình chữ nhật là lấy tích hai kích thước. Hay bằng cách đo chu vi các đĩai gỗ bằng dây, một học sinh có thể suy ra rằng chu vi đường tròn lớn hơn ba lần đường kính đường tròn một chút.

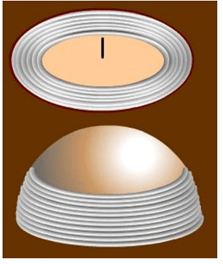
Và đây là một ví dụ cao cấp hơn, hãy xét một đĩa gỗ ở tâm có đóng một đinh sâu đến nửa và một bán cầu cùng bán kính, ở cực cũng có một chiếc định như thế.   Bây giờ ta cuộn một sợi dây thừng bắt đầu từ chiếc đinh và theo hình xoắc ốc cho đến khi lấp đầy đĩa tròn và bán cầu (Trong hình chỉ vẽ một phần sợi dây). Vì sợi dây thừng lấp đầy bán cầu dài gấp hai sợi dây thừng lấp đầy đỉa tròn nên ta kết luận diện tích bán cầu bằng hai lần diện tích hình tròn cùng bán kính, do đó diện tích mặt cầu bằng bốn diện tích hình tròn lớn của nó – một sự kiện đã được Archimedes chứng minh một cách nghiên nhặt vào thế kỉ thứ ba trước công nguyên. Với các thực nghiệm như thế, hình học đã trở thành một khoa học thực nghiệm.

Hình học trong giai đoạn thí nghiệm này được gọi là hình học thực nghiệm. Khi lục lọi sâu vào lịch sử toán học trong quá khứ, chúng ta tìm thấy một số lượng đáng kể những kết quả của hình học thực nghiệm. Loại hình học này hình như đã xuất hiện trong vài vùng phát triển ở phương Đông Cổ Đại trong khoảng thiên niên kỉ thứ năm đến thứ ba trước công nguyên qua quá trình xây dựng, trồng trọt, thương mại cũng như những nghi lễ tôn giáo.

Thật thú vị khi biết rằng mọi kiến thức hình học còn lưu giữ được trước 600 trước công nguyên phần lớn đều là hình học thực nghiệm. Hình học hình thành bằng một số qui tắc thô sơ, một số đúng đắn, một số chỉ gần đúng, như hình học của Babylon, Ai cập và Ấn độ, cũng như Trung quốc. Để minh họa, ta hãy xét công thức tính diện tích hình viên phân của Trung quốc.

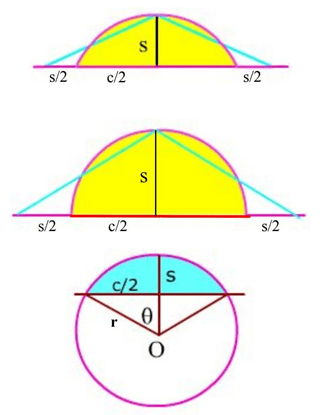
Công thức này được tìm thấy trong bộ Cửu Chương Toán Pháp, có nguồn gốc từ thế kỉ thứ hai trước Công nguyên, nhưng ta biết Tần Thủy Hoàng có chính sách đốt sách năm 213 trước Công nguyên, cho nên có thể tin quyển sách này có nguồn gốc sớm hơn nữa. Hình viên phân là hình giới hạn bởi hình tròn và một dây cung của nó (phần tô màu xanh hay vàng trong hình trên). Trong hình trên,  gọi c là độ dài của dây cung và s là chiều cao của viên phân. Nếu từ đỉnh của viên phân ta kẻ hai cát tuyến cắt phần kéo dài của c một đoạn bằng với s/2, bằng mắt thường ta thấy hình như diện tích hình viên phân bằng diện tích tam giác cân tạo bởi đường c và hai cát tuyến. Cửu chương Toán Pháp cho rằng hai diện tích này bằng nhau tức công thức diện tích hình viên phân theo sách đó là:

A = s(c + s)/2

 Áp dụng công thức này cho hình viên phân đặc biệt là nửa hình tròn bán kính r (Hình trên giữa) : c = 2r, s = r, ta được diện tích nửa hình tròn là :

A = r(2r + r)/2 = 3r²/2,

tức diện tích hình tròn là 3r², trong khi diện tích hình tròn đúng là Πr² Như vậy Cửu Chương Toán Pháp đã cho Π = 3, một giá trị gần đúng của Π thường dùng trong thời cổ.

Cách tính chính xác diện tích hình viên phân theo hai đại lượng c và s tương đối khá phức tạp, ngay cả đối với học sinh lớp 10. Diện tích viên phân là hiệu diện tích hình quạt tròn và diện tích tam giác cân đỉnh O. Như vậy diện tích hình viên phân là:

r²  θ – ( r²sinθ )/2

Để tính r, có thể áp dụng định lý Pythagoras cho tam giác vuông có ba cạnh r, c/2 và (r – s)

r²  = (c/2)² + (r – s)²

Và sau một hồi tính toán ta được:

r = (4s² + c²)/8s

Còn góc θ tính từ : sinθ = c/2r: đúng là không đơn giản.

Trong bản giấy cói Rind ghi lại công trình hình học của người Ai cập có niên đại ít nhất 1650 TCN chúng ta tìm thấy qui tắc tính diện tích hình tròn bằng diện tích hình vuông có độ dài cạnh bằng 8/9 đường kính hình tròn. Như thế công thức thực nghiệm này cho rằng giá trị của số  Π = (4/3)⁴ = 3,1604…

Mặc dù phần lớn các thổ bản bằng đất sét khô đào được ở Mesopotamia chứng tỏ rằng người Baylon lấy  Π  = 3, một thổ bản có niên đại từ 1900 đến 1600 TCN khai quật được ở Susa năm 1936, cách thành phố Babylon 200 dặm cho Π = 3¹/₈ = 3,125.

Còn nhiều dẫn chứng khác nữa về loại hình học thực nghiệm này. Chúng ta rất ấn tượng trước số lượng đồ sộ của các qui tắc được tìm thấy bằng các phương pháp thuần túy thực nghiệm.

Nếu giữa số lượng kiến thức ấy, chúng ta phải tìm một ví dụ nổi bật nhất để minh họa một thời khắc trọng đại của toán học, không có ví dụ nào tốt hơn là Bài toán số 14 trong bản giấy cói Moskow. Bản này có niên đại khoảng 1850 TCN trên đó ghi lại 25 bài toán cổ. Bản giấy cổ này được mua ở Ai cập năm 1893 và hiện giờ được lưu giữ trong một bảo tàng ở Moscow. Trong Bài toán 14, ta tìm thấy một thuật toán như sau: “Bạn được cho một khối chóp cụt có chiều cao 6, cạnh đáy lớn 4, cạnh đáy nhỏ 2. Bạn bình phương 4 được 16, nhân 4 cho 2 được 8, bình phương 2 được 4. Sau đó bạn cộng 3 số này là 16, 8 và 4, được 28. Rồi lấy một phần ba của 6 là 2. Cuối cùng nhân 28 với 2 được 56. Thế, số 56 đó chính là thể tích của khối chóp cụt. Bạn sẽ thấy kết quả rất đúng.”

Bạn hiểu việc này như thế nào? Đầu tiên, chúng ta phải biết rằng, theo thói quen thời cổ khi minh họa các bài toán, trước tiên một thủ tục tổng quát được đưa ra, sau đó là những con số cụ thể cá biệt được áp dụng. Vì mọi khối chóp Ai cập thời cổ đều có dạng khối chóp tứ giác đều nên bài toán đề cập đến khối chóp cụt tứ giác đều, là phần của khối chóp đều cắt bởi một mặt phẳng song song với đáy. Gọi a, b lần lượt là cạnh đáy và h là chiều cao thì ở đây: a = 4, b = 2 và h = 6. Từ mô tả trên, thuật toán này cho rằng thể tích khối chóp cụt tứ giác đều là V = (a² + ab + b²)h/3, một kết quả cá biệt của một công thức tổng quát hơn cho một khối chóp cụt bất kì là :

trong đó B, B’, h lần lượt là diện tích hai đáy và chiều cao của khối chóp cụt.

Hãy ngừng một lúc, nếu lí giải của chúng ta là đúng, để bày tỏ sự thán phục của chúng ta với công thức tìm được bằng thực nghiệm này. Chúng ta biết rằng người Babylon đã tìm ra công thức diện tích của hình thang (coi như tam giác “cụt”) bằng tích chiều cao và nửa tổng của hai cạnh đáy. Từ đó người Babylon cho rằng thể tích khối chóp cụt cũng bằng tích chiều cao với nửa tổng diện tích hai đáy, nghĩa là : V = h (B₁ + B₂)/2

Ức đoán này cũng tự nhiên và có vẻ triển vọng nhưng thật ra lại sai.

Tác giả người Ai cập thời cổ của Bài toán 14 trong bản thảo Moscow, không giống như những người Babylon, lại đoán chính xác. Rõ ràng sự qui nạp này là một thành quả thực nghiệm đáng nể trong hình học. Đáng nể đến nổi nhà toán học Eric Temple Bell đã đặt tên cho Bài toán 14 là ” kim tự tháp Ai cập vĩ đại nhất”; với Bell, phép qui nạp mà bài toán đưa ra đáng nể hơn nhiều so với công trình xây dựng các kim tự tháp khổng lồ bằng đá tảng của Ai cập cổ đại còn đứng vững đến tận ngày nay. Đây chính là một thời khắc trọng đại của toán học.